Informação mínima para fechamento de balanços¶
Neste problema, busca-se o conhecimento da informação mínima para o fechamento de balanços materiais que resultam em sistemas lineares. Um problema prático associado é a localização de sensores, conforme segue.
Problema - Localização de Sensores¶
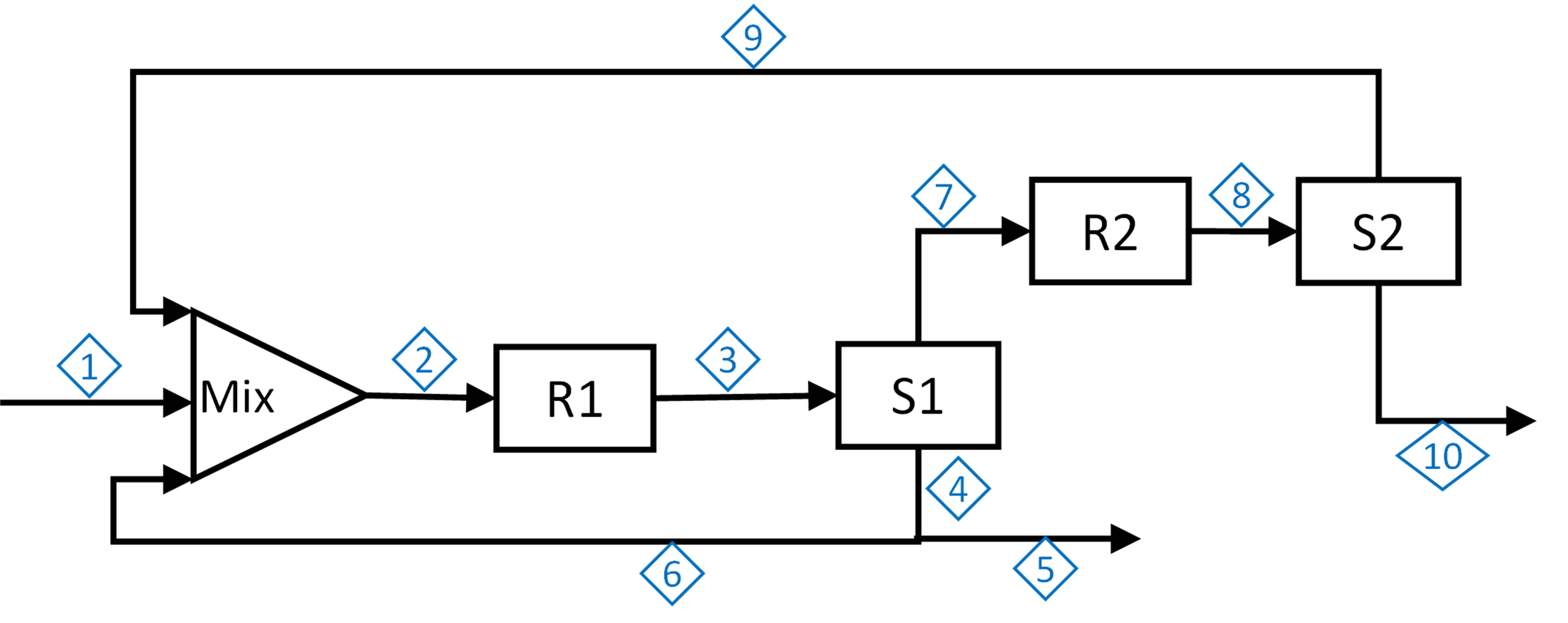
Deve-se inserir sensores para medição da vazão mássica total (em kg/s). Monte o sistema, analise o posto e, por escalonamento, indique em que posições se deveria inserir sensores para medir a vazão de forma que possamos estimar todas as vazões de todas as correntes.
Solução¶
Considerando o sistema, podemos inserir os balanços
$$ \begin{array}{c} \hline \rm{Mix} \\ \dot{M}_{1} + \dot{M}_{6}+ \dot{M}_{9} = \dot{M}_{2} \\ \hline \rm{Reator \ R1} \\ \dot{M}_{3} = \dot{M}_{2} \\ \hline \rm{Separador \ S1} \\ \dot{M}_{3} = \dot{M}_{4} + \dot{M}_{7} \\ \hline \rm{Tê \ de \ divisão} \\ \dot{M}_{4} = \dot{M}_{5} + \dot{M}_{6} \\ \hline \rm{Reator \ R2} \\ \dot{M}_{7} = \dot{M}_{8} \\ \hline \rm{Separador \ S2} \\ \dot{M}_{8} = \dot{M}_{9} + \dot{M}_{10} \\ \hline \end{array} $$Rescrevendo o sistema, temos:
$$ \begin{array}{ccc} \hline \dot{M}_{1} - \dot{M}_{2} + \dot{M}_{6}+ \dot{M}_{9} & =& 0 \\ \dot{M}_{2} - \dot{M}_{3} & =& 0 \\ \dot{M}_{3} - \dot{M}_{4} - \dot{M}_{7} & =& 0 \\ \dot{M}_{4} - \dot{M}_{5} - \dot{M}_{6} & = & 0 \\ \dot{M}_{7} - \dot{M}_{8} & = & 0 \\ \dot{M}_{8} - \dot{M}_{9} - \dot{M}_{10} & = & 0 \\ \hline \end{array} $$Ou escrito na forma de um sistema linear: $$ \begin{array}{ccc} \underbrace{ \begin{pmatrix} 1 & -1 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & -1 & 0 & 0 & -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & -1 & -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & -1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & -1 & -1 \end{pmatrix} }_{\mathbf{A}} & \cdot \underbrace{ \begin{pmatrix} \dot{M}_1 \\ \dot{M}_2 \\ \dot{M}_3 \\ \dot{M}_4 \\ \dot{M}_5 \\ \dot{M}_6 \\ \dot{M}_7 \\ \dot{M}_8 \\ \dot{M}_9 \\ \dot{M}_{10} \\ \end{pmatrix} }_{\mathbf{x}} & = \underbrace{ \begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{pmatrix} }_{\mathbf{y}} \end{array} $$
Ou em termos matriciais simplificados
$$ \mathbf{A} \cdot \mathbf{x} = \mathbf{y} $$Podemos agoram montar a matriz estendida:
$$ \mathbf{M} = \left( \begin{array}{c:c} \mathbf{A} & \mathbf{y} \end{array} \right) $$$$ \mathbf{M} = \left( \begin{array}{c:c} \begin{matrix} 1 & -1 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & -1 & 0 & 0 & -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & -1 & -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & -1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & -1 & -1 \end{matrix} & \begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{matrix} \end{array} \right) $$Agora podemos efetuar o escalonamento da matriz. Mediante o escalonamento da matriz estendida, obtemos (vamos apenas rotular a que as colunas se referem):
$$ \mathbf{Mesc} = \begin{array}{cccccccccc|c} \dot{M}_1 & \dot{M}_2 & \dot{M}_3 & \dot{M}_4 & \dot{M}_5 & \dot{M}_6 & \dot{M}_7 & \dot{M}_8 & \dot{M}_9 & \dot{M}_{10} & \rm{Lado \ direito} \\ \hline 1&0&0&0&-1&0&0&0&0&-1&0\cr 0&1&0&0&-1&-1&0&0&-1&-1&0\cr 0&0&1&0&-1&-1&0&0&-1&-1&0\cr 0&0&0&1&-1&-1&0&0&0&0&0\cr 0&0&0&0&0&0&1&0&-1&-1&0\cr 0&0&0&0&0&0&0&1&-1&-1&0\cr \end{array} $$A análise do resultado está apresentada na figura a seguir:
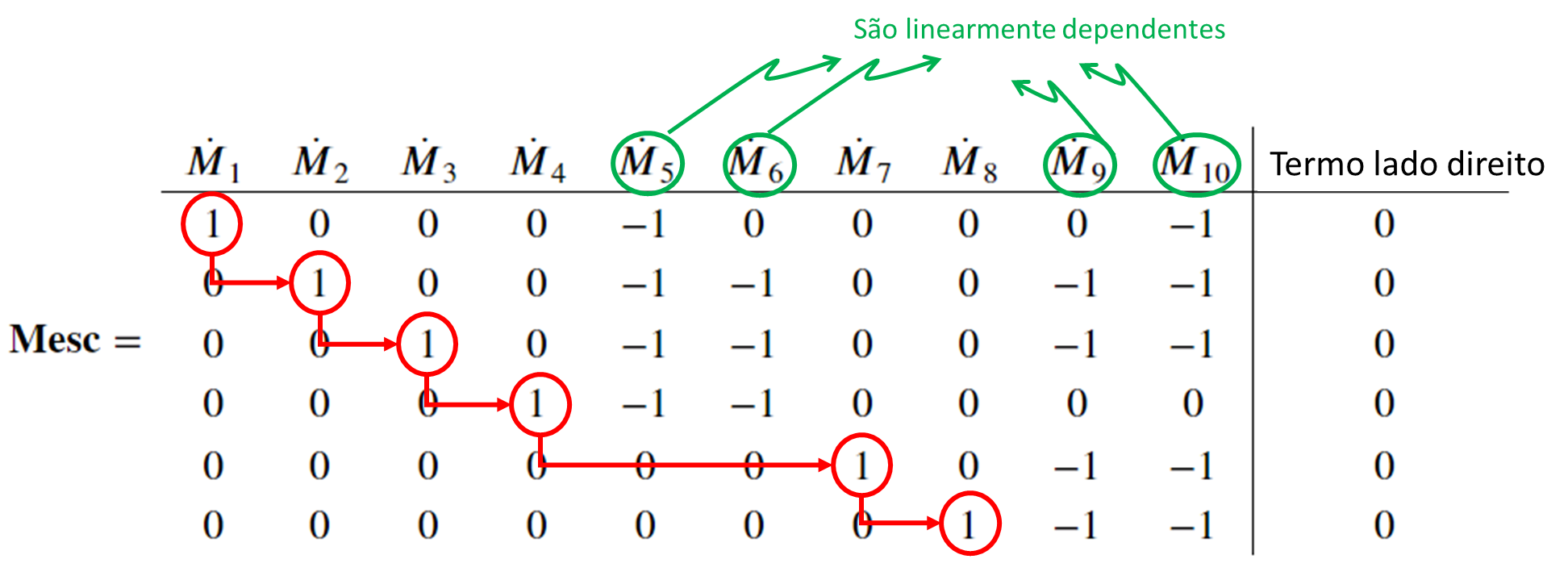
A análise indica que as colunas $ \dot{M}_5 $, $ \dot{M}_6 $, $ \dot{M}_9 $, $ \dot{M}_{10} $ apresentam dependência linear das demais colunas. Consequementemente, se conhecêssemos os valores de $ \dot{M}_5 $, $ \dot{M}_6 $, $ \dot{M}_9 $, $ \dot{M}_{10} $, poderíamos calcular as demais vazões. Então, sensores poderiam ser colocados nas correntes $ \dot{M}_5 $, $ \dot{M}_6 $, $ \dot{M}_9 $, $ \dot{M}_{10} $, neste exemplo.
Do ponto de vista de sistema linear, podemos re-escrever, a partir da forma escalonada, o sistema como:
$$ \begin{pmatrix}1&0&0&0&0&0\cr 0&1&0&0&0&0\cr 0&0&1&0&0&0\cr 0&0&0&1&0&0\cr 0&0&0&0&1&0\cr 0&0&0&0&0&1\cr \end{pmatrix} \cdot \begin{pmatrix} \dot{M}_1 \\ \dot{M}_2 \\ \dot{M}_3 \\ \dot{M}_4 \\ \dot{M}_7 \\ \dot{M}_8 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{pmatrix} - \begin{pmatrix}-1&0&0&-1\cr -1&-1&-1&-1\cr -1&-1&-1&-1\cr -1&-1&0&0\cr 0&0&-1&-1\cr 0&0&-1&-1\cr \end{pmatrix} \cdot \begin{pmatrix} \dot{M}_5 \\ \dot{M}_6 \\ \dot{M}_9 \\\dot{M}_{10} \end{pmatrix} $$Ou de forma mais simplificada:
$$ \begin{pmatrix} \dot{M}_1 \\ \dot{M}_2 \\ \dot{M}_3 \\ \dot{M}_4 \\ \dot{M}_7 \\ \dot{M}_8 \end{pmatrix} = - \begin{pmatrix}-1&0&0&-1\cr -1&-1&-1&-1\cr -1&-1&-1&-1\cr -1&-1&0&0\cr 0&0&-1&-1\cr 0&0&-1&-1\cr \end{pmatrix} \cdot \begin{pmatrix} \dot{M}_5 \\ \dot{M}_6 \\ \dot{M}_9 \\\dot{M}_{10} \end{pmatrix} $$Ou ainda:
$$ \begin{pmatrix} \dot{M}_1 \\ \dot{M}_2 \\ \dot{M}_3 \\ \dot{M}_4 \\ \dot{M}_7 \\ \dot{M}_8 \end{pmatrix} = - \begin{pmatrix}-1\cr -1\cr -1\cr -1\cr 0\cr 0\cr \end{pmatrix} \cdot \dot{M}_5 - \begin{pmatrix} 0\cr -1\cr -1\cr -1\cr 0\cr 0\cr \end{pmatrix} \cdot \dot{M}_6 - \begin{pmatrix}0\cr -1\cr -1\cr 0\cr -1\cr -1\cr \end{pmatrix} \cdot \dot{M}_9 - \begin{pmatrix}-1\cr -1\cr -1\cr 0\cr -1\cr -1\cr \end{pmatrix} \cdot \dot{M}_{10} $$O problema acima estipula um das possíveis soluções para a localização dos sensores para o fechamento do balanço material. Esta solução provavelmente não é a ótima. Outros fatores como comportamento dos erros experimentais de medição e propagação de erros devem ser considerados para escolha ótima (não visto aqui).