Universidade do Estado do Rio de Janeiro
Instituto de Química
Prof André Luís Alberton

Índice

Espaço vetorial e espaço nulo

Espaço Vetorial

Sejam dois vetores linearmente independentes $\overrightarrow{u}$ e $\overrightarrow{v}$. Estes dois vetores formam um plano no $ \mathbf{R}^2 $. Este plano contém todos o conjunto de todos os vetores que podem resultar da combinação linear de $ \overrightarrow{u} $ e $ \overrightarrow{v} $. Em termos matemáticos, o plano é chamado de espaço vetorial (span)dos vetores $\overrightarrow{u}$ e $\overrightarrow{v}$. Ou seja, um vetor $\overrightarrow{y}$ pertencerá à tal espaço vetorial se puder ser escrito como:

$$\overrightarrow{y} = x_1 \cdot \overrightarrow{u} + x_2 \cdot \overrightarrow{v} $$

em que $ x_1, x_2 $ são escalares. Podemos dar um nome a tal espaço vetorial, por exemplo, $ \mathbb{U} $. Em termos matemáticos:

$$ x_1 \cdot \overrightarrow{u} + x_2 \cdot \overrightarrow{v} \in \mathbb{U}, \ \forall \ x_1,x_2 \in \ \mathbf{R}, \\ \ \mathbb{U} = span \{ \overrightarrow{u}, \overrightarrow{v} \} $$

Vejamos um exemplo.

Exemplo 1 -) Visualizando o espaço vetorial

Considere os vetores $\overrightarrow{u}$ e $\overrightarrow{v}$ a seguir:

$$ \overrightarrow{u} = \begin{pmatrix}0.849\cr 0.685\cr 0.878\cr \end{pmatrix}, \ \overrightarrow{v} = {\begin{pmatrix}0.068\cr 0.56\cr 0.662\cr \end{pmatrix}} $$

Represente o espaço vetorial formado pelos vetores $\overrightarrow{u}$ e $\overrightarrow{v}$:

Solução

O código de Scilab que gera o plano está apresentado a seguir:

f = get("current_figure");
f.figure_position = [-8,-8];
f.figure_size = [1936,1056];

// Função que plota os vetores,
// p(2 ou 3) - numérico, vetor com os pontos finais do vetor a ser plotado
// nome - texto com o nome do vetor
// cor - inteiro, indicando a cor do vetor
// p0(2 ou 3) - numérico, vetor com os pontos iniciais do vetor; se não informado, assume que o ponto inicial é a origem
function plotaseta(p,nome,cor,p0)
    if length(p)==3 then
        if p0<>[] then
            xarrows([p0(1),p(1)],[p0(2),p(2)],[p0(3),p(3)],1,cor)
        else
            xarrows([0,p(1)],[0,p(2)],[0,p(3)],1,cor)
        end
    elseif length(p)==2 then
        if p0<>[] then
            xarrows([p0(1),p(1)],[p0(2),p(2)],1,cor)
        else
            xarrows([0,p(1)],[0,p(2)],1,cor)
        end
    end

    e=gce();
    e.thickness=.5;e.arrow_size=2;
    xstring(1,1,'$\ '+nome+ '$')
    e = gce()
    e.data=[p'];e.font_size=5
    e.font_foreground=cor
endfunction

// Vetores que formam a base
u = [0.849 ; 0.685;  0.878]
v = [0.068; 0.56; 0.662]

// Limites do plano representado
xmin = -2.5; xmax =2.5;
ymin = -2.5; ymax = 2.5

// Gera os limites da grade
xy = [xmin   xmin   xmax   xmax  xmin
      ymin   ymax   ymax   ymin  ymin]

// Número de pontos da grade
npts = 22
dx = (ymax-ymin)/(npts-1)
dy = (xmax-xmin)/(npts-1)
for i=1:npts
    aux = (ymin+dx*(i-1))
    gradey = [xmin xmax; aux aux]
    gradey3d = [u v]*gradey
    param3d(gradey3d(1,:),gradey3d(2,:),gradey3d(3,:))   
    e=gce();
    e.thickness=.25;e.foreground=7; 

    aux = (ymin+dy*(i-1))
    gradex = [aux aux;ymin ymax]
    gradex3d = [u v]*gradex
    param3d(gradex3d(1,:),gradex3d(2,:),gradex3d(3,:)) 
    e=gce();
    e.thickness=.25;e.foreground=7;
end

// Plota a grade
uvw = [u v]*xy
param3d(uvw(1,:),uvw(2,:),uvw(3,:))

// Plota o eixo canônico
cor = 1
plotaseta([1 0 0]',"e_{1}",cor,[])
plotaseta([0 1 0]',"e_{2}",cor,[])
plotaseta([0 0 1]',"e_{3}",cor,[])

// Plota os vetores u,v
cor = 9
plotaseta(u,'\overrightarrow{u}',cor,[])
plotaseta(v,'\overrightarrow{v}',cor,[])

a= gca()
a.box="off"
a.axes_visible = ["off","off","off"]
a.data_bounds = [-1, -1, -1; 1,1,1]*1
a.x_label.visible="off"
a.y_label.visible="off"
a.z_label.visible="off"

O espaço vetorial formado pelos vetores $\overrightarrow{u}$ e $\overrightarrow{v}$ está apresentado a seguir.

Figura - Plano Vetorial $ \mathbb{U}= span \left( \overrightarrow{u}, \overrightarrow{v} \right) $, um subespaço $ \mathbf{R}^2 $ do espaço $ \mathbf{R}^3 $ (o espaço $ \mathbf{R}^3 $ é representado pela base canônica $ \overrightarrow{e_1},\overrightarrow{e_2},\overrightarrow{e_3} $ )

__ Fim do Exemplo

Agora que entendemos o que é $ \mathcal{U} $, podemos explorar algumas características.

Dimensão e base de um espaço vetorial

Vamos definir o que é dimensão de um espaço vetorial:

$$ \rm{A \ dimensão \ de \ um \ espaço \ vetorial \ \mathcal{U} \ é \ igual \ ao \ número \ de \ vetores \ LI \ que \\ compõem \ uma \ base \ para \ \mathcal{U} } $$

Vimos que no exemplo apresentado, $ \mathcal{U} $ é formado a partir de $\overrightarrow{u}$ e $\overrightarrow{v}$, sendo 2 vetores linearmente indepenentes, resultando em um plano $\mathbf{R}^2$. Dizemos então que a dimensão de $\mathcal{U} $ é 2, pois é formado por 2 vetores LI.

$$ \rm{se} \ \mathcal{U} = \mathbf{R}^m ,\ \rm{então} \ dim \left( \mathcal{U} \right) = m, \ \rm{neste \ exemplo, \ m = 2} $$

No exemplo visto, os vetores $\overrightarrow{u}$ e $\overrightarrow{v}$ são ditos base do espaço vetorial $ \mathcal{U} $. A base de $ \mathcal{U} $ deve composta por vetores linearmente independentes. A base de $ \mathcal{U} $ não é única; e quaisquer n vetores LI do espaço vetorial $ \mathcal{U} $ poderiam ser base deste espaço.

$$ \rm{Uma \ base \ de } \ \mathcal{U} \ \rm{ pode \ ser \ composta \ por \ quaisquer \ m \ vetores \ LI \ de} \ \mathcal{U} \, \rm{onde} \ dim \left(\mathcal{U} \right) = m $$

Como a base de um espaço vetorial não é única, é muitas vezes conveniente escolher uma base ortogonal para este espaço. No scilab, o comando orth retorna o espaço vetorial ortogonal de uma matriz cujos vetores colunas formam a base do espaço vetorial analisado.

Exemplo 2-) Escrevendo o espaço vetorial em uma base ortogonal

Considere os vetores $\overrightarrow{u}$ e $\overrightarrow{v}$ a seguir:

$$ \overrightarrow{u} = \begin{pmatrix}0.849\cr 0.685\cr 0.878\cr \end{pmatrix}, \ \overrightarrow{v} = {\begin{pmatrix}0.068\cr 0.56\cr 0.662\cr \end{pmatrix}} $$

a-) Determine uma base ortogonal para o espaço vetorial formado pelos vetores $\overrightarrow{u}$ e $\overrightarrow{v}$:

b-) Mostre que o vetor $ \overrightarrow{y} = 0,5 \cdot \overrightarrow{u} + 0,6 \cdot \overrightarrow{v} $ pode ser escrito em termos da base ortogonal obtida.

Solução

a-) No Scilab, a solução fica:

u = [0.849 ; 0.685;  0.878]
v = [0.068; 0.56; 0.662]
B = orth([u,v])
disp(B)

  -0.4831459   0.873633 
  -0.5469377  -0.3526665
  -0.6836879  -0.3352489

A matriz $ \mathbf{B} $ terá em suas colunas a base ortogonal, ou seja:

$$ \mathbf{B} = \begin{pmatrix}-0.4831459&0.873633\cr -0.5469377&-0.3526665\cr -0.6836879&-0.3352489\cr \end{pmatrix} = \begin{pmatrix} | & | \\ \overrightarrow{b_1^c} & \overrightarrow{b_2^c} \\ | & | \end{pmatrix} $$

A solução resulta nos vetores da base $ \overrightarrow{b_1} $ e $ \overrightarrow{b_2} $ (eles não são os únicos possíveis, ok?):

$$ \overrightarrow{b_1} = {\begin{pmatrix}-0.4831459\cr -0.5469377\cr -0.6836879\cr \end{pmatrix}} $$$$ \overrightarrow{b_2} = {\begin{pmatrix}0.873633\cr -0.3526665\cr -0.3352489\cr \end{pmatrix}} $$

Ou seja, o espaço vetorial $ \mathbb{U} $ pode ser escrito em termos da base $ \overrightarrow{b_1} $ , $ \overrightarrow{b_2} $, ou $ \overrightarrow{u} $, $ \overrightarrow{v} $, ou quaisquer dois vetores LI do plano $ \mathbb{U} $ define.

$ \mathbb{U} = span \left( \overrightarrow{b_1}, \overrightarrow{b_2} \right) = span \left( \overrightarrow{u}, \overrightarrow{v} \right) $

A vantagem de $ \overrightarrow{b_1}, \overrightarrow{b_2} $ é que esta base é ortogonal, já que o produto interno entre tais vetores é nulo:

$$ \overrightarrow{b_1}^T \cdot \overrightarrow{b_2} = \sum_{i=1}^3{\overrightarrow{b_{1,i}} \cdot \overrightarrow{b_{2,i}} } = -0.4831459 \cdot 0.873633 + \left(-0.5469377 \right) \cdot \left(-0.3526665 \right) + \left( -0.6836879 \right) \cdot \left( -0.3352489 \right) = 0 $$

Observe que o mesmo plano é definido pelos vetores $ \overrightarrow{b_1}, \overrightarrow{b_2} $ e $ \overrightarrow{u}, \overrightarrow{v} $, conforme figura a seguir. No entanto, os vetores $ \overrightarrow{b_1}, \overrightarrow{b_2} $ apresentam como vantagens serem ortogonais entre si.

Figura - Plano Vetorial $ \mathbb{U}= span \left( \overrightarrow{u}, \overrightarrow{v} \right) = span \left( \overrightarrow{b_1}, \overrightarrow{b_2} \right) $

b-) Vamos primeiro obter o vetor $ \overrightarrow{y} $:

$$ \overrightarrow{y} = 0.5 \cdot \overrightarrow{u} + 0.6 \cdot \overrightarrow{v} = 0.5 \cdot {\begin{pmatrix} 0.849\cr 0.685 \cr -0.878\cr \end{pmatrix}} + 0.6 \cdot \begin{pmatrix}0.068\cr 0.56\cr 0.662\cr \end{pmatrix} = \begin{pmatrix}0.4653\cr 0.6785\cr 0.8362\cr \end{pmatrix} $$

Agora, queremos escrever o vetor $ \overrightarrow{y} $ em termos dos vetores $ \overrightarrow{b_1} $ e $ \overrightarrow{b_2} $:

$$ x_1 \cdot \overrightarrow{b_1} + x_2 \cdot \overrightarrow{b_2} = \overrightarrow{y} $$$$ {\begin{pmatrix}-0.4831459\cr -0.5469377\cr -0.6836879\cr \end{pmatrix}} \cdot x_1 + {\begin{pmatrix}0.873633\cr -0.3526665\cr -0.3352489\cr \end{pmatrix}} \cdot x_2 = \begin{pmatrix}0.4653\cr 0.6785\cr 0.8362\cr \end{pmatrix} $$

O que pode ser escrito na forma de um sistema linear como:

$$ \begin{pmatrix}-0.4831459&0.873633\cr -0.5469377&-0.3526665\cr -0.6836879&-0.3352489\cr \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix}0.4653\cr 0.6785\cr 0.8362\cr \end{pmatrix} $$

Que pode ser resolvido para se encontrar $ x_1,x_2$. Usando o Scilab para solução, com o comando linsolve, temos:

u = [0.849 ; 0.685;  0.878]
v = [0.068; 0.56; 0.662]
B = orth([u,v])
y = .5*u+.6*v
x = linsolve(B,-y)

O que retorna o resultado de $ x_1, x_2 $ de:

$$ \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix}-1.1676049\cr -0.1131179\cr \end{pmatrix} $$

Ou seja, o mesmo vetor $\overrightarrow{y}$ pode ser escrito em termos de $ \overrightarrow{b_1}, \overrightarrow{b_2} $ ou de $\overrightarrow{u}, \overrightarrow{v}$. Encontrar os multiplicadores da base vetorial que geram o vetor $\overrightarrow{y}$ consiste na solução do sistema linear.

Figura - Vetor $\overrightarrow{y} \in \mathbb{U} $

___Fim do Exemplo

Espaço Nulo

Considere o espaço vetorial $ \mathcal{U} =\mathbb{R}^m $ de dimensão $ m $, subespaço de um espaço vetorial $ \mathbb{R}^n $. O espaço nulo, também chamado de kernel ou núcleo de $ \mathcal{U} $ corresponde ao espaço vetorial ortogonal à $ \mathcal{U} $ que completa o $ \mathbb{R}^n $. As dimensões dos espaços vetorial e do espaço nulo somam a dimensão do espaço completo $ \mathbb{R}^n $, ou seja:

$$ \underbrace{\rm{dim} \left( \mathcal{U} \right)}_{m} + \rm{dim} \ kernel \left( \mathcal{U} \right) = \underbrace{ \rm{dim} \mathbb{R}^n }_{n} $$$$ \rm{dim} \ kernel \left( \mathcal{U} \right) = n - m $$

Por exemplo, considere $ \mathcal{U} $ como o espaço formado pelos vetores $\overrightarrow{u}$ e $\overrightarrow{v}$, designado por $\mathcal{U}$. O espaço vetorial $\mathcal{U}$ define um espaço $ \mathbb{R}^2 $, que é subespaço de um espaço vetorial $ \mathbb{R}^3 $. O conjunto de todos os vetores perpendiculares a $\mathcal{U}$ é definido como espaço nulo de $\mathcal{U}$ corresponde ao kernel de $\mathcal{U}$. A dimensão do núcleo ou kernel de $\mathcal{U}$ é portanto:

$$\rm{dim} \ kernel \left( \mathcal{U} \right) = 3 - 2 = 1 $$

Dois vetores são ortogonais entre si se seu produto interno é nulo $ \left< *, * \right>=0 $. Com isto, se um vetor $\overrightarrow{w}$ for ortogonal à $\overrightarrow{u}$ e $\overrightarrow{v}$, então, ele pertence ao espaço nulo de $\mathcal{U}$. Ou seja, considere um vetor $\overrightarrow{w}$ tal que:

$$ \left< \overrightarrow{w} , \overrightarrow{u} \right> =0 $$$$ \left< \overrightarrow{w}, \overrightarrow{v} \right> =0 $$$$ \rm{então} \ \overrightarrow{w} \in kernel \left( \mathcal{U} \right) $$

Se os vetores forem escritos como vetores coluna, então o produto interno pode ser escrito na forma:

$$ \left< \overrightarrow{w} , \overrightarrow{u} \right> = \overrightarrow{w}^T \cdot \overrightarrow{u} = \sum_i{w_i \cdot u_i } $$

No scilab, as decomposições qr e svd permitem obter base do espaço nulo de uma matriz cujos vetores colunas formam a base do espaço vetorial analisado.

Exemplo 4 - Determinando uma base para o espaço nulo

Considere os vetores $ \overrightarrow{u} , \overrightarrow{v} $, sendo $ \mathbb{U} = span \left( \overrightarrow{u}, \overrightarrow{v} \right) $ a seguir:

$$ \overrightarrow{u} = \begin{pmatrix}0.849\cr 0.685\cr 0.878\cr \end{pmatrix}, \ \overrightarrow{v} = {\begin{pmatrix}0.068\cr 0.56\cr 0.662\cr \end{pmatrix}} $$

Determine uma base para o espaço nulo de $\mathbb{U}$ :

Solução Como os vetores $ \overrightarrow{u},\overrightarrow{v} $ são ambos vetores com 3 elementos, o espaço vetorial total é o $ \mathbf{R}^3 $. Vimos que $ \overrightarrow{u},\overrightarrow{v} $ expandem um $ \mathbf{R}^2 $ dentro do $ \mathbf{R}^3 $. O espaço-nulo de $ \mathbb{U} $ tem portanto, dimensão igual a 1. O vetor perpendicular ao espaço vetorial $\mathbb{U}$ pode ser obtido pelo produto vetorial entre os vetores $ \overrightarrow{u}, \overrightarrow{v} $ (o produto vetorial vale apenas para o $ \mathbf{R}^3 $).

$$ \overrightarrow{w} = \overrightarrow{u} \times \overrightarrow{v} $$$$ \overrightarrow{w} =\begin{pmatrix}-0.03821\cr -0.502334\cr 0.42886\cr \end{pmatrix} $$

Plotando o vetor:

Figura - Vetor $\overrightarrow{w} $ como base do $ kernel \ \left( \mathbb{U} \right) $

Nota: Embora tenhamos ilustrado para o mundo 3D, que é até onde enxergamos, os conceitos de espaço vetorial e espaço nulo se aplicam a dimensões quaisquer. Outras operações matemáticas não se aplicam, como por exemplo, o produto vetorial (que só se aplica para a 3° e 7° dimensão). Para generalizar a obtenção dos espaços vetoriais e espaços nulos, é conveniente tratarmos de decomposições como a decomposição QR e a decomposição SVD.

__ Fim do Exemplo

Decomposição SVD

A decomposição SVD decompõe uma matriz $\mathbf{A}$ de $ n \times m $ em uma matriz ortogonal quadrada $\mathbf{U}$ de $ n \times n $, uma matriz diagonal $\mathbf{\Sigma}$ de $ n \times m $ e uma matriz ortogonal quadrada $\mathbf{V}$ de $ m \times m $, ou seja:

$$ \underbrace{\mathbf{A}}_{n \times m} = \underbrace{\mathbf{U}}_{n \times n} \cdot \underbrace{\mathbf{\Sigma}}_{n \times m} \cdot \underbrace{\mathbf{V}^T}_{m \times m} $$

A matriz $ \mathbf{A} $ possui posto $ p $. As matrizes podem ser entendidas como, em que $ \alpha $ representa o espaço vetorial e $ \beta $ representa o espaço nulo:

$$ \mathbf{U} = \left( \begin{matrix} \underbrace{ \mathbf{U_{\alpha}}}_{n \times p} & | & \underbrace{ \mathbf{U_{\beta} } }_{n \times n-p} \end{matrix} \right) $$$$ \mathbf{\Sigma} = \left( \begin{matrix} \underbrace{ \mathbf{\Sigma_{\alpha}}}_{p \times p} & \underbrace{ \mathbf{0 }}_{p \times m-p } \\ \underbrace{ \mathbf{0 }}_{n-p \times p } & \underbrace{ \mathbf{0 }}_{n-p \times m-p } \end{matrix} \right) $$$$ \mathbf{V} = \left( \begin{matrix} \underbrace{ \mathbf{V_{\alpha}}}_{m \times p} & | & \underbrace{ \mathbf{V_{\beta} } }_{m \times m-p} \end{matrix} \right) $$

A matriz $ \mathbf{U_{\alpha}} $ contém o espaço vetorial coluna da matriz $ \mathbf{A} $; a matriz $ \mathbf{U_{\beta}} $ contém o espaço nulo coluna da matriz $ \mathbf{A} $.

A matriz $ \mathbf{\Sigma_{\alpha}} $ contém os valores singulares associados a decomposição da matriz $ \mathbf{A} $.

A matriz $ \mathbf{V_{\alpha}} $ contém o espaço vetorial linha da matriz $ \mathbf{A} $; a matriz $ \mathbf{V_{\beta}} $ contém o espaço nulo linha da matriz $ \mathbf{A} $.

A matriz original pode ser recomposta apenas pela sua parte vetorial, ou seja:

$$ \mathbf{A} = \mathbf{U_{\alpha}} \cdot \mathbf{S_{\alpha}} \cdot \mathbf{V_{\alpha}}^T $$

Vejamos alguns exemplos.

Exemplo -) Decomposição de uma matriz em valores e vetores singulares

Analise a seguinte matriz:

$$ \mathbf{A} = {\begin{pmatrix}0.01&0.21&0.045&0.69&0.09&0.13\cr 0.18&0.57&0.168&0.76&0.95&0.96\cr 0.49&0.26&0.199&0.35&0.22&0.65\cr 0.007&0.147&0.0315&0.483&0.063&0.091\cr 0.94&0.91&0.464&0.54&0.81&0.52\cr \end{pmatrix}} $$

Solução

Uma primeira observação da matriz diz respeito às suas dimensões: 5 linhas e 6 colunas. Há 6 vetores coluna para descrever um espaço que é no máximo $\mathbf{R}^5$, e 5 vetores linha para descrever um espaço que é no máximo $\mathbf{R}^6$. Esta primeira análise sugere haver uma "sobra de colunas" e um "déficit de linhas". Contudo, sabemos que:

$$ \rm{nº \ de \ colunas \ LI \ da \ matriz} \ \mathbf{A} = \rm{nº \ de \ linhas \ LI \ da \ matriz} \ \mathbf{A} = \rm{posto \ da \ matriz} \ \mathbf{A} $$

Nesta primeira:

• análise do espaço coluna indica que numericamente há uma coluna a mais; contudo, não sabemos ainda se os 6 vetores do espaço coluna expandem o $\mathbf{R}^5$, pois pode haver ainda mais dependência de colunas.
• a análise do espaço linha indica que o espaço linhas é incapaz de representar o $\mathbf{R}^6$, contudo, não sabemos se as 5 linhas são de fato LI.

O código a seguir em Scilab contém a decomposição para análise do sistema.

A = [0.01    0.21    0.045    0.69    0.09    0.13 
     0.18    0.57    0.168    0.76    0.95    0.96 
     0.49    0.26    0.199    0.35    0.22    0.65 
     0.007   0.147   0.0315   0.483   0.063   0.091
     0.94    0.91    0.464    0.54    0.81    0.52 ]
// tolerância (valores abaixo serão considerados nulos)
tol = 1e-10
// Dimensão de A
[n,m] = size(A) 
// Decomposição svd
[U,S,V,rk] = svd(A)
// Zera valores próximos a nulo
U(abs(U)<tol)=0
S(abs(S)<tol)=0
V(abs(V)<tol)=0
// Retorna os espaços vetorial e nulo coluna
U_alpha = U(:,1:rk) 
U_beta  = U(:,rk+1:n)
// Retorna os valores singulares
S_alpha = S(1:rk,1:rk)
// Retorna os espaços vetorial e nulo linha
V_alpha = V(:,1:rk) 
V_beta  = V(:,rk+1:m)

O primeiro resultado analisado é o posto da matriz, que no código acima é a variável rk, resultante da decomposição SVD. Para este exemplo, o posto = 4, o que significa que há apenas 4 linhas e 4 colunas LI na matriz $\mathbf{A}$. Isto significa que a matriz expande apenas um $\mathbf{R}^4 $, tanto no espaço linha quanto no espaço coluna. Apesar de haver 6 colunas, duas delas são LD das demais; e apesar de haver 5 linhas, 1 dela é LD das demais.

Os resultados da matrizes levam a:

$$ \mathbf{U} = \left( \begin{matrix} \underbrace{ \begin{matrix}-0.2021069&-0.4949065&-0.6180863&0.0577113\cr -0.6200225&-0.4826188&0.5658379&-0.2499573\cr -0.3477132&0.1044036&0.1164198&0.9244684\cr -0.1414748&-0.3464346&-0.4326604&0.0403979\cr -0.658639&0.6254835&-0.3115256&-0.2791361 \end{matrix}}_{ \mathbf{U_{\alpha}} } & \underbrace{ \begin{matrix}0.5734623\cr 0\cr 0\cr -0.8192319\cr 0 \end{matrix} }_{\mathbf{U_{\beta}} } \end{matrix} \right) $$$$ \mathbf{\Sigma} = \begin{pmatrix}2.5635181&0&0&0&0&0\cr 0&0.8013566&0&0&0&0\cr 0&0&0.5629679&0&0&0\cr 0&0&0&0.397247&0&0\cr 0&0&0&0&0&0\cr \end{pmatrix} $$$$ \mathbf{V} = \left( \begin{matrix} \underbrace{ \begin{matrix}-0.3526855&0.6799305&-0.254272&0.3687107\cr -0.4316018&0.2076303&-0.2204223&-0.3475666\cr -0.192126&0.2455052&-0.1203661&0.0410999\cr -0.4510863&-0.6255659&-0.5913207&0.106221\cr -0.4782952&0.0059344&0.4048851&-0.6354673\cr -0.4692284&-0.2072282&0.5988986&0.571366\cr \end{matrix}}_{ \mathbf{V_{\alpha}} } & \underbrace{ \begin{matrix}-0.0865022&-0.4530155\cr 0.6882822&0.3570555\cr -0.5921326&0.7321316\cr -0.1576336&-0.1392732\cr -0.3380192&-0.2986485\cr 0.1704662&0.1506112\cr \end{matrix} }_{\mathbf{V_{\beta}} } \end{matrix} \right) $$

A matriz original pode ser recomposta apenas pela sua parte vetorial. De fato:

$$ \mathbf{A} = \mathbf{U_{\alpha}} \cdot \mathbf{S_{\alpha}} \cdot \mathbf{V_{\alpha}}^T $$$$ \mathbf{A} = \begin{pmatrix}-0.2021069&-0.4949065&-0.6180863&0.0577113\cr -0.6200225&-0.4826188&0.5658379&-0.2499573\cr -0.3477132&0.1044036&0.1164198&0.9244684\cr -0.1414748&-0.3464346&-0.4326604&0.0403979\cr -0.658639&0.6254835&-0.3115256&-0.2791361 \end{pmatrix} \cdot \begin{pmatrix}2.5635181&0&0&0\cr 0&0.8013566&0&0\cr 0&0&0.5629679&0\cr 0&0&0&0.397247\cr \end{pmatrix} \cdot \begin{pmatrix}-0.3526855&0.6799305&-0.254272&0.3687107\cr -0.4316018&0.2076303&-0.2204223&-0.3475666\cr -0.192126&0.2455052&-0.1203661&0.0410999\cr -0.4510863&-0.6255659&-0.5913207&0.106221\cr -0.4782952&0.0059344&0.4048851&-0.6354673\cr -0.4692284&-0.2072282&0.5988986&0.571366\cr \end{pmatrix}^T $$

Vejamos a aplicação desta decomposição na análise do sistema linear

O sistema linear

Seja um sistema linear conforme representado abaixo:

$$ \mathbf{A} \cdot \overrightarrow{x} = \overrightarrow{y} $$

Ou em sua forma aberta matricialmente:

$$ \left( \begin{matrix} a_{1,1} & a_{1,2} & ... & a_{1,m} \\ a_{2,1} & a_{2,2} & ... & a_{2,m} \\ ... & ... & ... & ... \\ a_{n,1} & a_{n,2} & ... & a_{n,m} \end{matrix} \right) \cdot \left( \begin{matrix} x_1 \\ x_2 \\ ... \\ x_m \end{matrix} \right) = \left( \begin{matrix} y_1 \\ y_2 \\ ... \\ y_n \end{matrix} \right) $$

Onde o vetor $ \overrightarrow{y} $ pertence aos reais de dimensão $ n $, e o vetor $ \overrightarrow{x} $ pertence aos reais de dimensão $ m $. Cada vetor coluna da matriz $ \mathbf{A} $ pertence aos reais de dimensão $ n $, e cada vetor linha da matriz $ \mathbf{A} $ pertence aos reais de dimensão $ m $.

$$ \overrightarrow{y} \in \mathcal{R}^n $$$$ \overrightarrow{a}^C_j \in \mathcal{R}^n \ , \ \forall \ j =1..m $$$$ \overrightarrow{x} \in \mathcal{R}^m $$$$ \overrightarrow{a}^L_i \in \mathcal{R}^m \ , \ \forall \ i =1..n $$

Contudo, não necessariamente o vetor $ \overrightarrow{y} $ pode assumir qualquer vetor no espaço $ \mathcal{R}^n $, pois isto depende do posto da matriz $ \mathbf{A} $. Para entender, podemos re-escrever o sistema linear como:

$$ \underbrace{ \left( \begin{matrix} a_{1,1} \\ a_{2,1} \\ ... \\ a_{n,1} \end{matrix} \right) }_{ \overrightarrow{a}_1^C } \cdot x_1 + \underbrace{ \left( \begin{matrix} a_{1,2} \\ a_{2,2} \\ ... \\ a_{n,2} \end{matrix} \right) }_{ \overrightarrow{a}_2^C } \cdot x_2 + ... + \underbrace{ \left( \begin{matrix} a_{1,m} \\ a_{2,m} \\ ... \\ a_{n,m} \end{matrix} \right) }_{ \overrightarrow{a}_m^C } \cdot x_m = \underbrace{ \left( \begin{matrix} y_1 \\ y_2 \\ ... \\ y_n \end{matrix} \right) }_{ \overrightarrow{y} } $$

Ou seja:

$$ \overrightarrow{a}_1^C \cdot x_1 + \overrightarrow{a}_2^C \cdot x_2 + ... + \overrightarrow{a}_m^C \cdot x_m = \overrightarrow{y} $$

Logo, da expressão acima, fica evidente que o vetor $ \overrightarrow{y} $ é combinação linear dos vetores coluna da matriz $ \mathbf{A} $. Ou seja, $ \overrightarrow{y} $ pertence ao espaço vetorial dos vetores coluna da matriz $ \mathbf{A} $:

$$\overrightarrow{y} \ \in \ span \left(\overrightarrow{a}_1^C ,\overrightarrow{a}_2^C, ..., \overrightarrow{a}_m^C \right) $$

Se os vetores coluna apresentarem alguma dependência linear e a dimensão do espaço vetorial $ \mathcal{U} $ será menor que $ m $, e sempre igual ao posto da matriz $ \mathbf{A} $. Ou seja, se o posto da matriz $ \mathbf{A} $ for igual a $ p $, $ \overrightarrow{y} $ estará restrito a um espaço vetorial $ \mathcal{R}^p $.

Na transformação linear $ \mathbf{A} \cdot \overrightarrow{x} = \overrightarrow{y} $, podemos entender que:

• o vetor $ \overrightarrow{x} $ pode ser qualquer vetor em um espaço $ \mathcal{R}^m $;
• contudo, o vetor $ \overrightarrow{y} $ está restrito a um espaço $ \mathcal{R}^p $, onde $ p $ é o posto da matriz $ \overrightarrow{A} $

Em termos matemáticos, pode-se escrever:

$$ T_\mathbf{A} : \ \ \overrightarrow{x} \rightarrow \overrightarrow{y} $$$$ T_\mathbf{A} : \ \ \mathcal{R}^m \rightarrow \mathcal{R}^n $$

Contudo, $ \mathcal{R}^n $ é apenas o contradomínio da transformação. A imagem da transformação, onde $ \overrightarrow{y} $ verdadeiramente estará contido pode ser "menor" do que $ \mathcal{R}^n $, e é obrigatoriamente igual a $ \mathcal{R}^p $, em que $ p $ é o posto da matriz $ \mathbf{A} $.

$$ Im \left( T_\mathbf{A} \right) = \mathcal{R}^p, \ p = \rm{posto \ da \ matriz } $$

Mas e o espaço vetorial definido pelos vetores linhas da matriz $ \mathbf{A} $? Bem, um teorema do cálculo estabelece que:

$$ \rm{nº \ de \ colunas \ LI \ da \ matriz} \ \mathbf{A} = \rm{nº \ de \ linhas \ LI \ da \ matriz} \ \mathbf{A} = \rm{posto \ da \ matriz} \ \mathbf{A} = p $$

Ou seja, a dimensão do espaço vetorial coluna é a mesma dimensão do espaço vetorial linha. Vamos definir:

• espaço vetorial coluna da matriz $ \mathbf{A} $ como $ \mathcal{U} $
• espaço vetorial linhada matriz $ \mathbf{A} $ como $ \mathcal{V} $

Então:

$$ dim \left( \mathcal{U} \right) = dim \left( \mathcal{V} \right) = p $$

Ou seja, ambos $ \mathcal{U} $, $ \mathcal{V} $ definem um $ \mathcal{R}^p $, não necessariamente o mesmo. Sabemos que são espaços de mesma dimensão são isomórficos; então os espaços vetoriais $ \mathcal{U} $, $ \mathcal{V} $ são isomórficos entre si. Isto signfica que um vetor $ \overrightarrow{x} $ que pertença a $ \mathcal{V} $ terá uma equivalência biunívoca com um vetor $ \overrightarrow{y} $ que pertença a $ \mathcal{U} $.

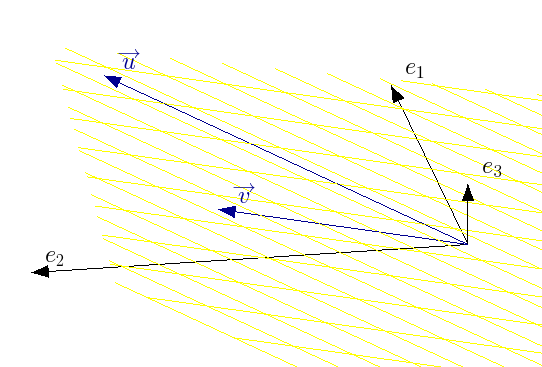
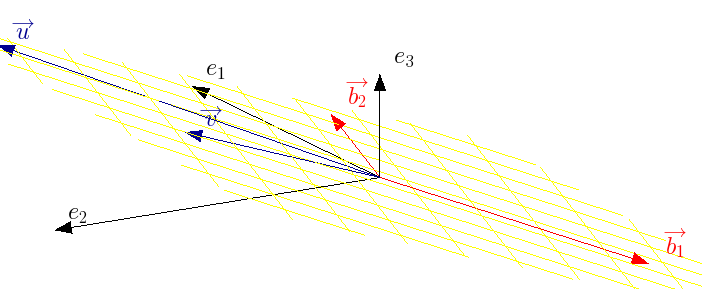
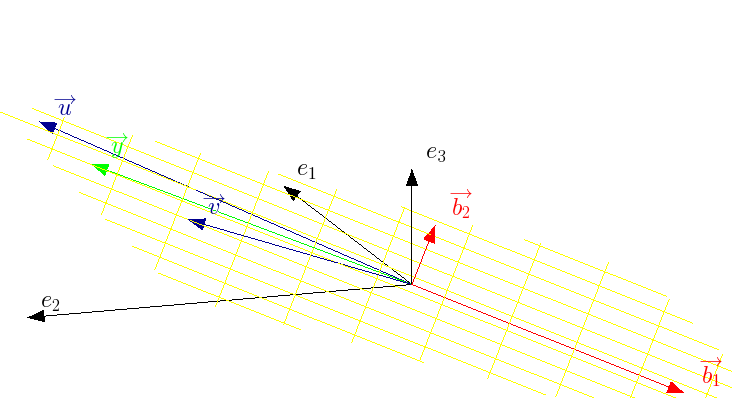
Para visualizar melhor, é conveniente observar bases ortogonais para os espaços linha e coluna, conforme segue.

Espaço vetorial coluna (pela decomposição svd)

Considere por exemplo, que escrevermos:

$$ \overrightarrow{y} = \mathbf{A} \cdot \overrightarrow{x} $$

Tomando a decomposição e sua parte vetorial, temos:

$$ \overrightarrow{y} = \mathbf{U_{\alpha}} \cdot \mathbf{S_{\alpha}} \cdot \mathbf{V_{\alpha}}^T \cdot \overrightarrow{x} $$$$ \overrightarrow{y} = \mathbf{U_{\alpha}} \cdot \mathbf{S_{\alpha}} \cdot \underbrace{ \left( \mathbf{V_{\alpha}}^T \cdot \overrightarrow{x} \right) }_{\overrightarrow{z}} $$$$ \overrightarrow{y} = \mathbf{U_{\alpha}}\cdot \cdot \mathbf{S_{\alpha}} \cdot \overrightarrow{z} $$$$ \overrightarrow{y} = \begin{pmatrix} | & | & | & | \\ \overrightarrow{u_{\alpha,1}} & \overrightarrow{u_{\alpha,2}} & \overrightarrow{u_{\alpha,3}} & \overrightarrow{u_{\alpha,4}} \\ | & | & | & | \end{pmatrix} \cdot \begin{pmatrix} \sigma_1 & 0 & 0 & 0 \cr 0 & \sigma_2 & 0 & 0 \cr 0 & 0 & \sigma_3 & 0 \cr 0 & 0 & 0 & \sigma_4 \end{pmatrix} \cdot \begin{pmatrix} z_1 \\ z_2 \\z_3 \\z_4 \end{pmatrix} $$$$ \overrightarrow{y} = z_1 \cdot \sigma_1 \cdot \begin{pmatrix} | \\ \overrightarrow{u_{\alpha,1}} \\ | \end{pmatrix} + z_2 \cdot \sigma_2 \cdot \begin{pmatrix} | \\ \overrightarrow{u_{\alpha,2}} \\ | \end{pmatrix} + z_3 \cdot \sigma_3 \cdot \begin{pmatrix} | \\ \overrightarrow{u_{\alpha,3}} \\ | \end{pmatrix} + z_4 \cdot \sigma_4 \cdot \begin{pmatrix} | \\ \overrightarrow{u_{\alpha,4}} \\ | \end{pmatrix} $$

Ou seja, o vetor $ \overrightarrow{y} $ pertence ao espaço vetorial dos vetores coluna de $ \mathbf{U_{\alpha}} $. Tudo bem, nada de novo, havíamos dito que a matriz $ \mathbf{U_{\alpha}} $ gera, em seus vetores coluna, o mesmo espaço vetorial gerado pelos vetores coluna da matriz $ \mathbf{A} $.

Os $ \sigma$ 's são ordenados tipicamente do maior para o menor: $ \sigma_1 > \sigma_2 > \sigma_3 > \sigma_4 $. Os $ \overrightarrow{u_{\alpha}} $'s são unitários. Assim, a direção que tipicamente mais "impacta" o vetor $ \overrightarrow{y} $ tende a ser a direção 1, seguida da direção 2, direção 3 e por fim a direção 4. Se o $ \sigma $ associado a uma direção for muito pequeno comparado aos demais, pode-se pensar que desprezar esta direção gera pouco impacto no vetor $\overrightarrow{y} $. De fato, isto fundamenta uma análise de grande importância na estatística: a análise dos componentes principais. Veremos a aplicação desta análise mais à frente na disciplina; por hora vamos nos contentar em entender que as direções $ \overrightarrow{u_{\alpha,}}'s $ representam as direções ortogonais que contém a informação do espaço vetorial coluna da matriz $ \mathbf{A} $.

Espaço vetorial linha (pela decomposição svd)

Na verdade, podemos observar isto pela decomposição em valores e vetores singulares da matriz $ \mathbf{A} $, considerando que vamos recuperar os $ \overrightarrow{x} $ que estão associados a transformação linear. Vamos designar por $ \overrightarrow{x}_{\alpha} $, porque como será mostrado, está associado ao espaço vetorial $ \mathcal{V} $. Então

$$ \mathbf{A} \cdot \overrightarrow{x}_{\alpha} = \overrightarrow{y} $$$$ \mathbf{U_{\alpha}} \cdot \mathbf{\Sigma_{\alpha}} \cdot \mathbf{V_{\alpha}}^T \cdot \overrightarrow{x}_{\alpha} = \overrightarrow{y} $$$$ \overrightarrow{x}_{\alpha} = \mathbf{V_{\alpha}} \cdot \mathbf{\Sigma_{\alpha}}^{-1} \cdot \mathbf{U_{\alpha}}^T \cdot \overrightarrow{y} $$

Chamando $ \overrightarrow{z} = \mathbf{U_{\alpha}}^T \cdot \overrightarrow{y} $, temos:

$$ \overrightarrow{x}_{\alpha} = \mathbf{V_{\alpha}} \cdot \mathbf{\Sigma_{\alpha}}^{-1} \overrightarrow{z} $$$$ \overrightarrow{x}_{\alpha} = \frac{z_1}{\sigma_1} \cdot \overrightarrow{v_1}_{\alpha} \cdot \frac{z_2}{\sigma_2} \cdot \overrightarrow{v_2}_{\alpha} + ... $$

Note que, se queremos obter $ \overrightarrow{x}_{\alpha} $ a partir de $ \overrightarrow{y} $, então pela equação acima, $ \overrightarrow{x}_{\alpha} \in span \left( \overrightarrow{v_1}_{\alpha}, \overrightarrow{v_2}_{\alpha}, ... \right) $, ou seja, $ \overrightarrow{x} \in \mathcal{V} $.

Entendendo as infinitas soluções

Vimos que qualquer vetor $ \overrightarrow{x}_{\alpha} $ pertencendo ao espaço vetorial linha da matriz $ \mathbf{A} $ tem uma relação biunívoca com um vetor $ \overrightarrow{y} $ que obrigatoriamente está no espaço vetorial coluna da matriz $ \mathbf{A} $. Contudo, algo realmente interessante surge quando observamos o espaço nulo linha da matriz $\mathbf{A} $, isto é, $ kernel \left( \mathcal{V} \right) $. Note que vetores que pertencem ao espaço nulo linha são ortogonais aos vetores linha da matriz $ \mathbf{A} $. Com isto, seja $ \overrightarrow{x}_{\beta} \in kernel \left( \mathcal{V} \right) $. Então:

$$ \mathbf{A} \cdot \overrightarrow{x}_{\beta} = \begin{pmatrix} - & \overrightarrow{a^L_1} & - \\ - & \overrightarrow{a^L_2} & - \\ - & ... & - \\ - & \overrightarrow{a^L_{n-1}} & - \\ - & \overrightarrow{a^L_n} & - \end{pmatrix} \cdot \overrightarrow{x}_{\beta} = \begin{pmatrix} \left< \overrightarrow{a^L_1}, \overrightarrow{x}_{\beta} \right> \\ \left< \overrightarrow{a^L_2}, \overrightarrow{x}_{\beta} \right> \\ ... \\ \left< \overrightarrow{a^L_{n-1}}, \overrightarrow{x}_{\beta} \right> \\ \left< \overrightarrow{a^L_n}, \overrightarrow{x}_{\beta} \right> \end{pmatrix} = \begin{pmatrix} 0 \cr 0 \cr ... \cr 0 \cr 0 \end{pmatrix} $$

Ou seja:

$$ \mathbf{A} \cdot \overrightarrow{x}_{\beta} = \overrightarrow{0}, \ \ \rm{se} \ \ \overrightarrow{x}_{\beta} \in \ kernel \left( \mathcal{V} \right) $$

Com isto, considere um problema com infinitas soluções, e com a solução $ \overrightarrow{x}_{\alpha} $ $$ \mathbf{A} \cdot \overrightarrow{x}_{\alpha} = \overrightarrow{y} $$

Tomando a relação anterior, para $ \overrightarrow{x}_{\beta} \in \ kernel \left( \mathcal{V} \right) $, temos:

$$ \mathbf{A} \cdot \overrightarrow{x}_{\alpha} = \overrightarrow{y} $$$$ \mathbf{A} \cdot \overrightarrow{x}_{\beta} = \overrightarrow{0} $$

Que somando leva a:

$$ \mathbf{A} \cdot \left( \overrightarrow{x}_{\alpha} + \overrightarrow{x}_{\beta} \right) = \overrightarrow{y} $$

Ou seja, $ \overrightarrow{x}_{\alpha} + \overrightarrow{x}_{\beta} $ também é solução do problema.

Podemos então entender qualquer solução particular $ \overrightarrow{x^*} $ em sua componente no espaço vetorial de $ \mathbf{V_{\alpha}} $ e no espaço nulo $ \mathbf{V_{\beta}} $.

Quando decompomos $ \mathbf{A} $ na decomposição svd, temos:

$$ \mathbf{A} \cdot \overrightarrow{x} = \overrightarrow{y} $$$$ \mathbf{U_{\alpha}} \cdot \mathbf{S_{\alpha}} \cdot \mathbf{V_{\alpha}}^T \cdot \overrightarrow{x} = \overrightarrow{y} $$

Ao multiplicar por $ \mathbf{U_{\alpha}}^T $, temos:

$$ \mathbf{U_{\alpha}}^T \cdot \mathbf{U_{\alpha}} \cdot \mathbf{S_{\alpha}} \cdot \mathbf{V_{\alpha}}^T \cdot \overrightarrow{x} = \mathbf{U_{\alpha}}^T \cdot \overrightarrow{y} $$

Ao multiplicar por $ \mathbf{S_{\alpha}}^{-1} $, temos:

$$ \mathbf{V_{\alpha}}^T \cdot \overrightarrow{x} = \mathbf{S_{\alpha}}^{-1} \cdot\mathbf{U_{\alpha}}^T \cdot \overrightarrow{y} $$

Por fim, ao multiplicar por $ \mathbf{V_{\alpha}} $, teremos obrigatoriamente o resultado projetado sobre o plano do espaço vetorial $ \mathcal{V} $.

$$ \underbrace{ \mathbf{V_{\alpha}} \cdot \mathbf{V_{\alpha}}^T \cdot \overrightarrow{x} }_{x_{\alpha}} = \mathbf{V_{\alpha}} \cdot \mathbf{S_{\alpha}}^{-1} \cdot\mathbf{U_{\alpha}}^T \cdot \overrightarrow{y} $$

O $ x_{\alpha} $ é a "parte fixa" da solução do problema. Podemos somar ao $ x_{\alpha} $ qualquer valor dentro do espaço nulo, que a solução permanece válida. Logo, a solução geral do problema linear fica:

$$ x = x_{\alpha} + \lambda_1 \cdot \overrightarrow{v}_1 + \lambda_2 \cdot \overrightarrow{v}_2 $$

, em que $ \overrightarrow{v}_1,\overrightarrow{v}_2 \in \ kernel \ \mathcal{V} $

Claramente, ao tomar um vetor no espaço nulo, sendo este ortogonal ao espaço vetorial $ \mathcal{V} $, estaremos apenas aumentando sua normal. Logo, o vetor solução de menor norma possível é o $ x_{\alpha} $.