Universidade do Estado do Rio de Janeiro
Instituto de Química
Prof André Luís Alberton

Índice

Sistemas lineares - Descrição e análise (com rotinas em Python)

Seja um sistema linear conforme representado abaixo:

$$ \mathbf{A} \cdot \overrightarrow{x} = \overrightarrow{y} $$

Ou em sua forma aberta matricialmente:

$$ \left( \begin{matrix} a_{1,1} & a_{1,2} & ... & a_{1,m} \\ a_{2,1} & a_{2,2} & ... & a_{2,m} \\ ... & ... & ... & ... \\ a_{n,1} & a_{n,2} & ... & a_{n,m} \end{matrix} \right) \cdot \left( \begin{matrix} x_1 \\ x_2 \\ ... \\ x_m \end{matrix} \right) = \left( \begin{matrix} y_1 \\ y_2 \\ ... \\ y_n \end{matrix} \right) $$

Ou alternativamente representado como:

$$ \underbrace{ \left( \begin{matrix} a_{1,1} \\ a_{2,1} \\ ... \\ a_{n,1} \end{matrix} \right) }_{ \overrightarrow{a}_1^C } \cdot x_1 + \underbrace{ \left( \begin{matrix} a_{1,2} \\ a_{2,2} \\ ... \\ a_{n,2} \end{matrix} \right) }_{ \overrightarrow{a}_2^C } \cdot x_2 + ... + \underbrace{ \left( \begin{matrix} a_{1,m} \\ a_{2,m} \\ ... \\ a_{n,m} \end{matrix} \right) }_{ \overrightarrow{a}_m^C } \cdot x_m = \underbrace{ \left( \begin{matrix} y_1 \\ y_2 \\ ... \\ y_n \end{matrix} \right) }_{ \overrightarrow{y} } $$

Ou seja:

$$ \overrightarrow{a}_1^C \cdot x_1 + \overrightarrow{a}_2^C \cdot x_2 + ... + \overrightarrow{a}_m^C \cdot x_m = \overrightarrow{y} $$

Logo, da expressão acima, fica evidente que o vetor $ \overrightarrow{y} $ é combinação linear dos vetores coluna da matriz $ \mathbf{A} $. Em termos matemáticos, o conjunto de todos os vetores que resultam da combinação linear dos vetores coluna da matriz é chamado de espaço vetorial coluna dos vetores coluna da matriz, também designado span. A base de um espaço vetorial é definida como um conjunto de vetores LI que formam tal espaço. A dimensão de um espaço vetorial é igual oa número de vetores LI que o definem, ou seja:

$$ \rm{ Uma \ base \ de \ um \ espaço \ vetorial \ é \ formada \ por \ vetores \ LI \ que definem \ tal \ espaço } $$$$ \rm{ A \ dimensão \ de \ um \ espaço \ vetorial \ é \ igual \ ao \ número \ de \ vetores \ LI \ que definem \ tal \ espaço } $$

Vamos também relembrar o posto de uma matriz. Temos que:

$$ \rm{nº \ de \ colunas \ LI \ da \ matriz} \ \mathbf{A} = \rm{nº \ de \ linhas \ LI \ da \ matriz} \ \mathbf{A} = \rm{posto \ da \ matriz} \ \mathbf{A} = p $$

Isto significa que o número de linhas e colunas LI da matriz $\mathbf{A}$ é o mesmo, definindo espaços vetoriais $ \mathbf{R}^p $, de dimensão $ p $. O valor de $ p $ é obrigatoriamente menor ou igual à menor dimensão da matriz, ou seja:

$$ n = \rm{nº \ de \ linhas \ da \ matriz } $$$$ m = \rm{nº \ de \ colunas \ da \ matriz } $$$$ p \leq menor \left( n,m \right) $$

A primeira análise dos sistemas lineares do tipo envolve a natureza do problema, como:

• com solução única => resolva
• com infinitas soluções => analise
• sem solução => se for o caso, encontre a solução mais próxima

No Python, o posto de uma matriz pode ser obtido com diversos pacotes. Um dos mais usuais uma rotina do pacote numpy que pode ser acessada com o comando np.linalg.matrix_rank() (onde np é a referência clássica à importação do pacote numpy)

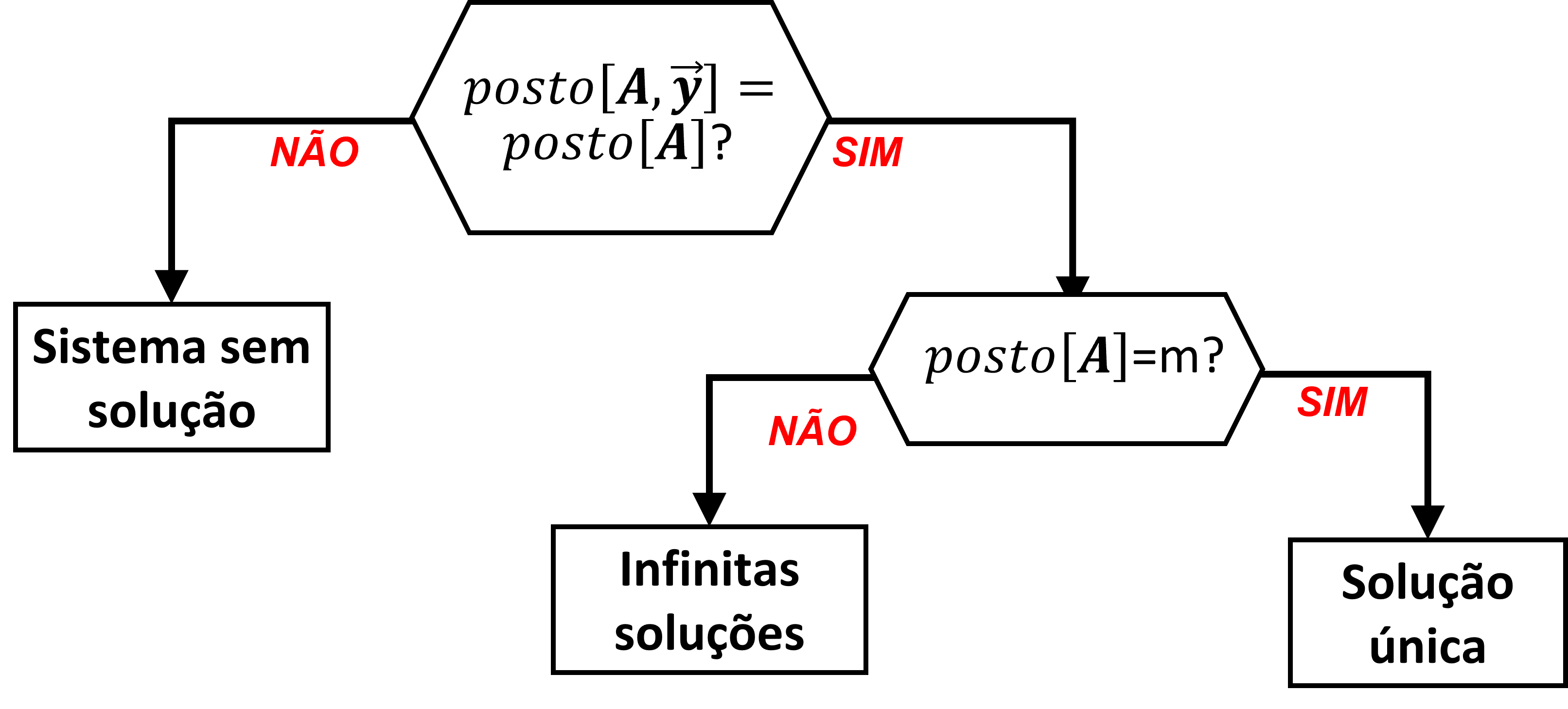
Solução única

O problema terá solução única se:

• o posto da matriz $ \mathbf{A} $ for igual ao número de colunas dela, i.e: $ p = m $ (ou seja, não há colunas linearmente dependente na matriz $ \mathbf{A} $), e
• o vetor $ \overrightarrow{y} $ pertencer ao espaço vetorial formado pelos vetores coluna da matriz $ \mathbf{A} $. Esta condição é garantida se o posto da matriz estendida $ \left[ \mathbf{A}, \overrightarrow{y} \right] $ for igual ao posto da matriz $ \mathbf{A} $, ou seja: $ posto \left( \left[ \mathbf{A}, \overrightarrow{y} \right] \right) = posto \left( \mathbf{A} \right) $

Infinitas soluções

O problema terá infinitas soluções se:

• o posto da matriz $ \mathbf{A} $ for menor que número de colunas dela, i.e: $ p < m $ (ou seja, HÁ colunas linearmente dependente na matriz $ \mathbf{A} $), e
• o vetor $ \overrightarrow{y} $ pertencer ao espaço vetorial formado pelos vetores coluna da matriz $ \mathbf{A} $. Esta condição é garantida se o posto da matriz estendida $ \left[ \mathbf{A}, \overrightarrow{y} \right] $ for igual ao posto da matriz $ \mathbf{A} $, ou seja: $ posto \left( \left[ \mathbf{A}, \overrightarrow{y} \right] \right) = posto \left( \mathbf{A} \right) $

Sem solução

O problema naõ terá solução se:

• o vetor $ \overrightarrow{y} $ NÃO pertencer ao espaço vetorial formado pelos vetores coluna da matriz $ \mathbf{A} $. Esta condição é garantida se o posto da matriz estendida $ \left[ \mathbf{A}, \overrightarrow{y} \right] $ for igual ao posto da matriz $ \mathbf{A} $, ou seja: $ posto \left( \left[ \mathbf{A}, \overrightarrow{y} \right] \right) > posto \left( \mathbf{A} \right) $

A figura a seguir ilustra a análise do sistema linear:

Figura - Análise do sistema linear $

No Python, esta análise pode ser feita conforme código a seguir:

# Entradas: matriz A; vetor y (o vetor y pode conter uma ou duas dimensões)
# Saídas: info (0 se solução única, 1 se infinitas soluções, 2 se sem solução); msg - mensagem quanto a característica da solução

import numpy as np

def analise(A,y):
    # pergunta se y é unidimensional ou não. Se for unidimensional, acrescenta uma dimensão (é importante para a concatenação na montagem da matriz estendida) 
    if y.ndim ==1:
        y2 = np.array([y])
    else:
        y2 = np.array(y)
        
    # Monta a matriz estendida
    M = np.concatenate((A,y2.T),axis=1)
    # Obtém os postos (ranks) da matriz A e estendida M
    rankA = np.linalg.matrix_rank(A) 
    rankM = np.linalg.matrix_rank(M) 
    # Pergunta se os ranks das matrizes A e M são iguais (se sim, há solução)
    if rankA == rankM:
         # Obtém o número de linhas e colunas da matriz A
        nlin, ncol = A.shape
        # Se o posto da matriz A é igual ao número de colunas, solução única
        if rankA==ncol:
            info = 0
            msg = "solucao unica"
        # Se o postos for diferente, há colunas de A 'sobrando' (infinitas soluções)
        else:
            info = 1
            msg = "infinitas solucoes"
    # se o posto da matriz A e M forem distintos, não há solução
    else:
        info = 2
        msg = "sem solucao"
    return([info,msg])        
        
# Exemplo    
A = np.array([[0.25,   5.06,   6.21,   5.31],
              [5.17,   4.23,   3.45,   9.4], 
              [3.91,   2.89,   7.06,   6.8], 
              [2.41,   0.88,   5.21,   3.29]])
       
y = np.array([[7.22,    8.97,    2.42,    4.33]])

[info,msg] = analise(A,y)
print(info)
print(msg)

2
sem solucao

Funções internas do Python

Para o seguinte sistema linear

$$ \mathbf{A} \cdot \overrightarrow{x} = \overrightarrow{y} $$

Dentre os comandos de solução do Python que podem ser úteis, inclui-se:

	Pacote	Solução única	Infinitas soluções	Sem solução
np.solve(A,y) $^1$	numpy	retorna a solução única	retorna uma solução	retorna valores espúrios, $[]$
np.linalg.pinv(A) @ y $^2 $	numpy	retorna a solução única	retorna solução de menor norma	retorna solução mais próxima (projeção de $ \overrightarrow{y} $ sobre o espaço vetorial coluna de $ \mathbf{A}$)
M.rref(iszerofunc=lambda x:abs(x)<1e-10)$^3$	simpy	conterá na última coluna a solução	permite obter as colunas LD e montar todas as soluções	pouco útil, retornará na última coluna uma parte da matriz identidade

1 - (np.solve é válido apenas para sistemas quadrados) 2 - para uso do np.linalg.pinv(A) @ y, a variável y deve ser de dimensão única 3 - no caso do sympy, M é um objeto simpy.Matrix. Além disto, deve ser informada uma tolerância, senão retorna lixos

Exemplos

Exemplo 1 - Solução única

Resolva o seguinte sistema linear:

$$ \begin{pmatrix}1&-1&3\cr 2&1&0\cr -4&3&-1\cr \end{pmatrix} \cdot \begin{pmatrix} x_1 \cr x_2 \cr x_3 \end{pmatrix} = \begin{pmatrix}0\cr -2\cr 5\cr \end{pmatrix} $$

Este problema tem solução única. O posto da matriz $ \mathbf{A} =3 $, a matriz é quadrada de 3x3. A solução pode ser obtida mediante diferentes comandos, como segue:

# Solução única
import sympy as sp
import numpy as np

A = np.array([[1, -1, 3],
             [2, 1, 0], 
             [-4, 3, -1]])

y = np.array([[0,-2,5]])
M = sp.Matrix([[1, -1, 3, 0],
               [2, 1, 0, -2], 
               [-4, 3, -1, 5]])

# Por numpy.solve (o y foi informado com duas dimensões, por isto, usa-se y[0])
xsol1 = np.linalg.solve(A,y[0])
print('pelo numpy.solve',xsol1)

# Por uso da pseudo inversa
xsol2 = np.linalg.pinv(A) @ y[0]
print('pelo uso de numpy.pinv',xsol2)

# Por escalonamento da matriz
Mred = M.rref(iszerofunc=lambda x:(abs(x)<1e-10) )
print('Matriz reduzida',Mred)

pelo numpy.solve [-1.14814815  0.2962963   0.48148148]
pelo uso de numpy.pinv [-1.14814815  0.2962963   0.48148148]
Matriz reduzida (Matrix([
[1, 0, 0, -31/27],
[0, 1, 0,   8/27],
[0, 0, 1,  13/27]]), (0, 1, 2))

Os resultados estão apresentados para a inversa de A e para o escalonamento a seguir:

$$ \overrightarrow{x} = \begin{pmatrix}-1.1481481\cr 0.2962963\cr 0.4814815\cr \end{pmatrix} $$

Ou pelo escalonamento reduzido (efetuando-se os cálculos de divisão)

$$ \begin{pmatrix}1&0&0&-1.1481481\cr 0&1&0&0.2962963\cr 0&0&1&0.4814815\cr \end{pmatrix} $$

Observe que, pelo escalonamento reduzido, a útlima coluna é igual a solução obtida pela inversa da matriz $ \mathbf{A} $ multiplicada pelo vetor $ \overrightarrow{y} $.

Exemplo 2 - Infinitas soluções

Considere o seguinte sistema linear:

$$ \begin{pmatrix}1&0&0.5&-5&-5.1\cr 3&2&2.3&2&1.7\cr 4&-1&1.6&3&2.6\cr -1&5&1.5&1&1.1\cr \end{pmatrix} \cdot \begin{pmatrix} x_1 \cr x_2 \cr x_3 \cr x_4 \cr x_5 \end{pmatrix} = \begin{pmatrix}-2.2\cr 2.7\cr 2.3\cr 2.2\cr \end{pmatrix} $$

A matriz $ \mathbf{A} $ e o vetor $ \mathbf{y} $ foram criados de acordo com a lógica:

$$ coluna 1 = \begin{pmatrix} 1 \cr 3 \cr 4 \cr -1 \end{pmatrix} $$$$ coluna 2 = \begin{pmatrix} 0 \cr 2 \cr -1 \cr 5 \end{pmatrix} $$$$ coluna 3 = 0.5 \cdot coluna 1 + 0.4 \cdot coluna 2 $$$$ coluna 4 = \begin{pmatrix}-5 \cr 2\cr 3 \cr 1 \end{pmatrix} $$$$ coluna 5 = coluna4- 0.1 \cdot coluna 1; $$$$ \mathbf{A} = [coluna 1, coluna 2, coluna 3, coluna 4, coluna 5] $$$$ \overrightarrow{y} = 0.3 \cdot coluna 1 + 0.4 \cdot coluna 2 + .5 \cdot coluna 4 $$

Este exemplo foi criado para ter infinitas soluções. Neste exemplo, trata-se de uma matriz $ \mathbf{A} $ com 4 linhas e 5 colunas, ou seja, $ n=4, \ m=5 $. Neste exemplo, as colunas 3 e 5 foram criadas de forma a gerar dependência com colunas anteriores. O vetor $ y $ foi criado como combinação linear das colunas 1, 2, e 4.

O código em Python está apresentado a seguir:

import numpy as np
import sympy as sp
# Escrita da matriz A e do vetor y
A = np.array([[1, 0, .5, -5, -5.1] , [3,2,2.3,2,1.7],[4,-1,1.6,3,2.6],[-1,5,1.5,1,1.1]])
y = np.array([[-2.2, 2.7, 2.3, 2.2]])
# Concatenação para obter a matriz estendida
M = np.concatenate((A,y.T),axis=1)
# Transforma a matriz estendida em um objeto do simpy
M = sp.Matrix(M)
# Utliza a função rref (é necessário informar a tolerância, senão o código faz caquinha)
Mred = M.rref(iszerofunc=lambda x:abs(x)<1e-10)

print('matriz reduzida', Mred)

matriz reduzida (Matrix([
[1, 0, 0.5, 0, -0.1, 0.3],
[0, 1, 0.4, 0,    0, 0.4],
[0, 0,   0, 1,  1.0, 0.5],
[0, 0,   0, 0,    0,   0]]), (0, 1, 3))

O resultado da matriz reduzida apresentado a seguir:

$$ \mathbf{M_{red}} = \begin{pmatrix} \color{red}{1} &0&0.5&0&-0.1&0.3\cr 0& \color{red}{1} &0.4&0&0&0.4\cr 0&0&0&\color{red}{1}&1&0.5\cr 0&0&0&0&0&0\cr \end{pmatrix} $$

Observe que as colunas que forma ajustadas como a matriz identidade foram as colunas $1, \ 2, \ 4$. As colunas $ 3, \ 5 $ da matriz são LD, assim como a coluna $ 6 $, referente ao termo do lado direito da equação. Além disto, a última linha não carrega nenhuma informação. Ou seja, o sistema linear pode ser reescrito como:

$$\begin{pmatrix}1&0&0\cr 0&1&0\cr 0&0&1\cr \end{pmatrix} \cdot \begin{pmatrix} x_1 \cr x_2 \cr x_4 \end{pmatrix} + \begin{pmatrix}0.5&-0.1\cr 0.4&0\cr 0&1\cr \end{pmatrix} \cdot \begin{pmatrix} x_3 \cr x_5 \end{pmatrix} = \begin{pmatrix}0.3\cr 0.4\cr 0.5\cr \end{pmatrix} $$

Ou então:

$$\begin{pmatrix}1&0&0\cr 0&1&0\cr 0&0&1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \cr x_2 \cr x_4 \end{pmatrix} = \begin{pmatrix}0.3\cr 0.4\cr 0.5 \end{pmatrix} -\begin{pmatrix}0.5&-0.1\cr 0.4&0\cr 0&1 \end{pmatrix} \cdot \begin{pmatrix} x_3 \cr x_5 \end{pmatrix} $$

A matriz identidade é o "1" da matemática vetorial; logo, pode ser omitida em uma multiplicação. Na forma escrita do sistema, as variáveis $ x_1, x_2, x_4 $ são chamadas de variáveis básicas e as variáveis $ x_3,x_5 $ são chamadas variáveis livres ou variáveis não-básicas.

$$ \underbrace{ \begin{pmatrix} x_1 \cr x_2 \cr x_4 \end{pmatrix} }_{\rm{variáveis \ básicas} } = \begin{pmatrix}0.3\cr 0.4\cr 0.5 \end{pmatrix} -\begin{pmatrix}0.5&-0.1\cr 0.4&0\cr 0&1 \end{pmatrix} \cdot \underbrace{ \begin{pmatrix} x_3 \cr x_5 \end{pmatrix} }_{\rm{variáveis \ livres}} $$

Ali estão todas as soluções do problema. Podemos assumir valores quaisquer de $ x_3,x_5 $ e calcular $ x_1, x_2, x_4 $.

Vale ressaltar que:

A escolha de variáveis básicas e livres não é única

Isto quer dizer que podemos trocar variáveis básicas e livres. Se a ordem das colunas fôssem diferentes, as variáveis básicas e livres seriam diferentes (por exemplo, poderíamos trocar $ x_2,x_3 $ dentre as variáveis básicas e livres neste exemplo).

Vale ressaltar o comando numpy.linalg.pinv neste exemplo. Tal comandos podem ser usados na forma:

# Pelo uso do numpy.linalg.pinv
xsol1 =  np.linalg.pinv(A) @ y[0]

print('pelo uso do numpy.linalg.pinv', xsol1)

pelo uso do numpy.linalg.pinv [0.20977539 0.30865942 0.22835146 0.26048877 0.23951123]

O resultado que retorna é:

$$ \overrightarrow{x} = \begin{pmatrix}0.2097754\cr 0.3086594\cr 0.2283515\cr 0.2604888\cr 0.2395112\cr \end{pmatrix} $$

Tal resultado é o resultado de menor norma possível para o vetor $ \overrightarrow{x}$ (lembrem-se que há infinitos resultados possíveis). O resultado de de menor norma possível pode ser de interesse ou não (geralmente não é, apenas em problemas específicos, importantes, mas específicos).

Exemplo 3 - Sistema sem solução

Considere o seguinte sistema linear:

$$ \begin{pmatrix}1&0&0.5&-5&-5.1\cr 3&2&2.3&2&1.7\cr 4&-1&1.6&3&2.6\cr -1&5&1.5&1&1.1\cr \end{pmatrix} \cdot \begin{pmatrix} x_1 \cr x_2 \cr x_3 \cr x_4 \cr x_5 \end{pmatrix} = \begin{pmatrix}-2.2\cr 2.7\cr 2.3\cr 2.6\cr \end{pmatrix} $$

Este é um sistema similar ao anterior; porém, contudo, sem solução.

Usando a forma escalonada reduzida, conforme segue:

# Sem solução
import numpy as np
import sympy as sp
A = np.array([[1, 0, .5, -5, -5.1] ,
              [3,2,2.3,2,1.7],
              [4,-1,1.6,3,2.6],
              [-1,5,1.5,1,1.1]])

y = np.array([[-2.2, 2.7, 2.3,2.6]])
M = np.concatenate((A,y.T),axis=1)
M =  sp.Matrix(M)
Mred = M.rref(iszerofunc=lambda x:abs(x)<1e-10)

print('matriz reduzida', Mred)

matriz reduzida (Matrix([
[1, 0, 0.5, 0, -0.1, 0],
[0, 1, 0.4, 0,    0, 0],
[0, 0,   0, 1,  1.0, 0],
[0, 0,   0, 0,    0, 1]]), (0, 1, 3, 5))

O resultado está apresentado a seguir:

$$ \mathbf{M_{red}} = \begin{pmatrix}\color{red}{1}&0&0.5&0&-0.1&0\cr 0&\color{red}{1}&0.4&0&0&0\cr 0&0&0&\color{red}{1}&1&0\cr 0&0&0&0&0&\color{red}{1}\cr \end{pmatrix} $$

Observe o resultado retorna como independentes as colunas $ 1 ,2, 4 ,6 $; porém, a coluna $ 6 $ é a coluna do termo independente; ou seja, o vetor $ \overrightarrow{y} $ não é formado pela combinação linear dos vetores colunas da matriz $ \mathbf{A} $; logo, o problema não tem solução.

O que podemos fazer nesta situação? Depende:

• se esperávamos que o problema tivesse solução, há algo errado.
• porém, há casos em que o problema é esperado não ter solução; como o caso da estimação de parâmetros no ajuste de modelos.

Se for este útimo caso, podemos encontrar a "solução mais próxima", com o uso da pseudo-inversa (comando numpy.linalg.pinv).

xsol = np.linalg.pinv(A) @ y[0]
print('uso do np.linalg.pinv',xsol)

uso do np.linalg.pinv [0.19340564 0.36767591 0.24377318 0.26115176 0.2418112 ]

Este comando retorna o resultado:

$$ \hat{\overrightarrow{x}} = \begin{pmatrix}0.1934056\cr 0.3676759\cr 0.2437732\cr 0.2611518\cr 0.2418112\cr \end{pmatrix} $$

O valor de $ \hat{\overrightarrow{y}} $ calculado a partir de $ \hat{\overrightarrow{x}} $ fica então:

$$ \hat{\overrightarrow{y}} = \mathbf{A} \cdot \hat{\overrightarrow{x}} = \begin{pmatrix}-2.2237037\cr 2.8096296\cr 2.2081481\cr 2.5377778\cr \end{pmatrix} $$

Este resultado de $ \hat{\overrightarrow{y}} $ representa a projeção ortogonal do vetor $ \overrightarrow{y} $ sobre o hiper-plano (espaço vetorial) formado pelos vetores coluna da matriz $ \mathbf{A} $.

Observe que o resíduo, a diferença entre o vetor $ \overrightarrow{y} - \hat{\overrightarrow{y}} $ é igual a:

residuo =  A @ xsol - y
print(residuo)

[[-0.0237037   0.10962963 -0.09185185 -0.06222222]]

O valor obitdo é:

$$ \hat{\overrightarrow{y}} - \overrightarrow{y} = \begin{pmatrix}-2.2\cr 2.7\cr 2.3\cr 2.6\cr \end{pmatrix} - \begin{pmatrix}-2.2237037\cr 2.8096296\cr 2.2081481\cr 2.5377778\cr \end{pmatrix} = {\begin{pmatrix}-0.0237037\cr 0.1096296\cr -0.0918519\cr -0.0622222\cr \end{pmatrix}} $$