Sistemas lineares - Descrição e análise (com rotinas em Scilab)¶
Seja um sistema linear conforme representado abaixo:
$$ \mathbf{A} \cdot \overrightarrow{x} = \overrightarrow{y} $$Ou em sua forma aberta matricialmente:
$$ \left( \begin{matrix} a_{1,1} & a_{1,2} & ... & a_{1,m} \\ a_{2,1} & a_{2,2} & ... & a_{2,m} \\ ... & ... & ... & ... \\ a_{n,1} & a_{n,2} & ... & a_{n,m} \end{matrix} \right) \cdot \left( \begin{matrix} x_1 \\ x_2 \\ ... \\ x_m \end{matrix} \right) = \left( \begin{matrix} y_1 \\ y_2 \\ ... \\ y_n \end{matrix} \right) $$Ou alternativamente representado como:
$$ \underbrace{ \left( \begin{matrix} a_{1,1} \\ a_{2,1} \\ ... \\ a_{n,1} \end{matrix} \right) }_{ \overrightarrow{a}_1^C } \cdot x_1 + \underbrace{ \left( \begin{matrix} a_{1,2} \\ a_{2,2} \\ ... \\ a_{n,2} \end{matrix} \right) }_{ \overrightarrow{a}_2^C } \cdot x_2 + ... + \underbrace{ \left( \begin{matrix} a_{1,m} \\ a_{2,m} \\ ... \\ a_{n,m} \end{matrix} \right) }_{ \overrightarrow{a}_m^C } \cdot x_m = \underbrace{ \left( \begin{matrix} y_1 \\ y_2 \\ ... \\ y_n \end{matrix} \right) }_{ \overrightarrow{y} } $$Ou seja:
$$ \overrightarrow{a}_1^C \cdot x_1 + \overrightarrow{a}_2^C \cdot x_2 + ... + \overrightarrow{a}_m^C \cdot x_m = \overrightarrow{y} $$Logo, da expressão acima, fica evidente que o vetor $ \overrightarrow{y} $ é combinação linear dos vetores coluna da matriz $ \mathbf{A} $. Em termos matemáticos, o conjunto de todos os vetores que resultam da combinação linear dos vetores coluna da matriz é chamado de espaço vetorial coluna dos vetores coluna da matriz, também designado span.
A base de um espaço vetorial é definida como um conjunto de vetores LI que formam tal espaço. A dimensão de um espaço vetorial é igual oa número de vetores LI que o definem, ou seja:
Vamos também relembrar o posto de uma matriz. Temos que:
$$ \rm{nº \ de \ colunas \ LI \ da \ matriz} \ \mathbf{A} = \rm{nº \ de \ linhas \ LI \ da \ matriz} \ \mathbf{A} = \rm{posto \ da \ matriz} \ \mathbf{A} = p $$Isto significa que o número de linhas e colunas LI da matriz $\mathbf{A}$ é o mesmo, definindo espaços vetoriais $ \mathbf{R}^p $, de dimensão $ p $. O valor de $ p $ é obrigatoriamente menor ou igual à menor dimensão da matriz, ou seja:
$$ n = \rm{nº \ de \ linhas \ da \ matriz } $$$$ m = \rm{nº \ de \ colunas \ da \ matriz } $$$$ p \leq menor \left( n,m \right) $$A primeira análise dos sistemas lineares do tipo envolve a natureza do problema, como:
- com solução única => resolva
- com infinitas soluções => analise
- sem solução => se for o caso, encontre a solução mais próxima
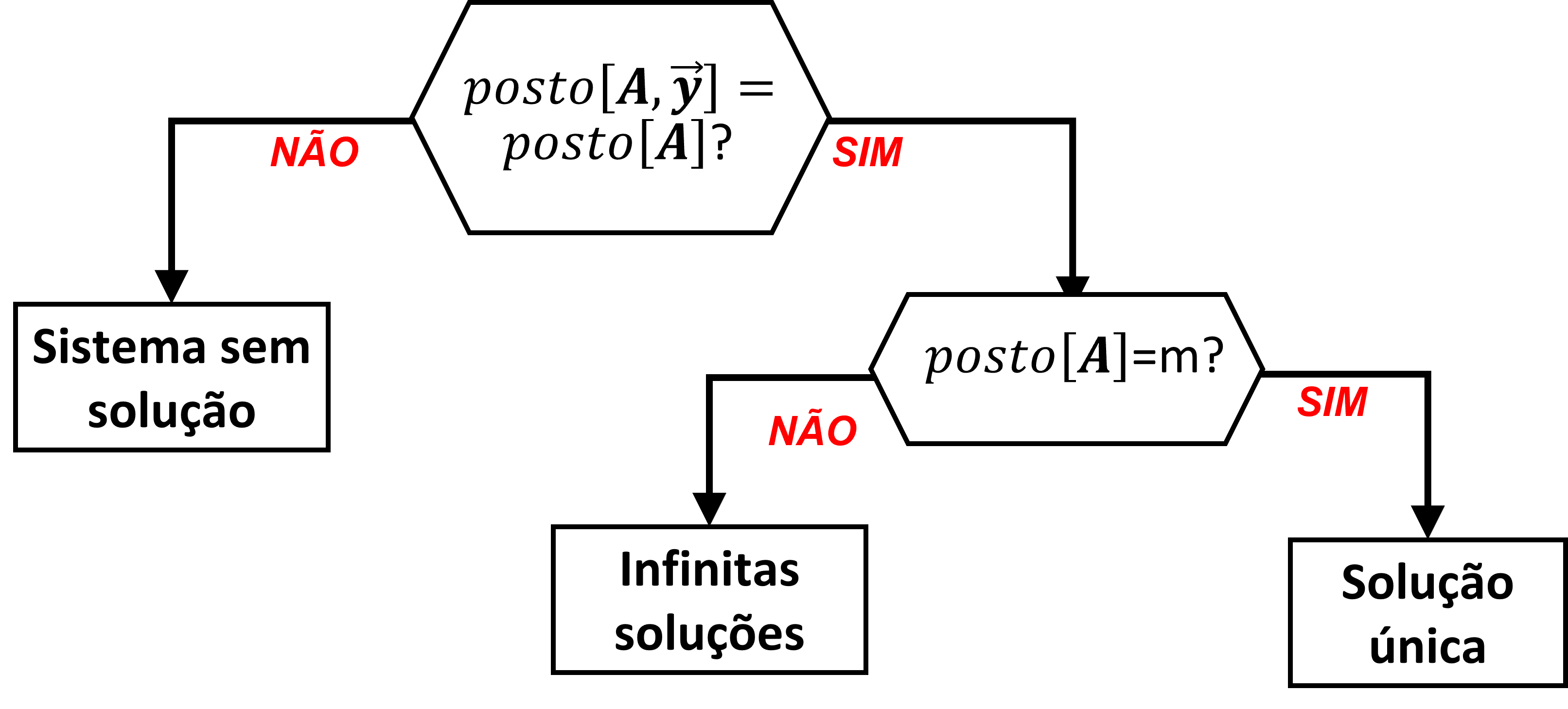
Solução única
O problema terá solução única se:
- o posto da matriz $ \mathbf{A} $ for igual ao número de colunas dela, i.e: $ p = m $ (ou seja, não há colunas linearmente dependente na matriz $ \mathbf{A} $), e
- o vetor $ \overrightarrow{y} $ pertencer ao espaço vetorial formado pelos vetores coluna da matriz $ \mathbf{A} $. Esta condição é garantida se o posto da matriz estendida $ \left[ \mathbf{A}, \overrightarrow{y} \right] $ for igual ao posto da matriz $ \mathbf{A} $, ou seja: $ posto \left( \left[ \mathbf{A}, \overrightarrow{y} \right] \right) = posto \left( \mathbf{A} \right) $
Infinitas soluções
O problema terá infinitas soluções se:
- o posto da matriz $ \mathbf{A} $ for menor que número de colunas dela, i.e: $ p < m $ (ou seja, HÁ colunas linearmente dependente na matriz $ \mathbf{A} $), e
- o vetor $ \overrightarrow{y} $ pertencer ao espaço vetorial formado pelos vetores coluna da matriz $ \mathbf{A} $. Esta condição é garantida se o posto da matriz estendida $ \left[ \mathbf{A}, \overrightarrow{y} \right] $ for igual ao posto da matriz $ \mathbf{A} $, ou seja: $ posto \left( \left[ \mathbf{A}, \overrightarrow{y} \right] \right) = posto \left( \mathbf{A} \right) $
Sem solução
O problema naõ terá solução se:
- o vetor $ \overrightarrow{y} $ NÃO pertencer ao espaço vetorial formado pelos vetores coluna da matriz $ \mathbf{A} $. Esta condição é garantida se o posto da matriz estendida $ \left[ \mathbf{A}, \overrightarrow{y} \right] $ for igual ao posto da matriz $ \mathbf{A} $, ou seja: $ posto \left( \left[ \mathbf{A}, \overrightarrow{y} \right] \right) > posto \left( \mathbf{A} \right) $
A figura a seguir ilustra a análise do sistema linear:
No Scilab, esta análise pode ser feita conforme código a seguir:
// Entradas: matriz A; vetor y
// Saídas: info (0 se solução única, 1 se infinitas soluções, 2 se sem solução); msg - mensagem quanto a característica da solução
function [info,msg] = analise(A,y)
if rank(A) == rank([A,y]) then
ncol = size(A,2)
if rank(A)==ncol then
info = 0
msg = "solucao unica"
else
info = 1
msg = "infinitas solucoes"
end
else
info = 3
msg = "sem solucao"
end
endfunction
A = [ 0.25 5.06 6.21 5.31
5.17 4.23 3.45 9.4
3.91 2.89 7.06 6.8
2.41 0.88 5.21 3.29 ]
y = [ 7.22; 8.97; 2.42; 4.33]
[info,msg] = analise(A,y)
Funções internas do Scilab¶
Para o seguinte sistema linear
$$ \mathbf{A} \cdot \overrightarrow{x} = \overrightarrow{y} $$Dentre as linhas de comando do Scilab que podem ser úteis, inclui-se:
| Solução única | Infinitas soluções | Sem solução | |
|---|---|---|---|
| linsolve(A,-y) | retorna a solução única | retorna solução de menor norma | retorna vazio, $[]$ |
| pinv(A) * y | retorna a solução única | retorna solução de menor norma | retorna solução mais próxima (projeção de $ \overrightarrow{y} $ sobre o espaço vetorial coluna de $ \mathbf{A}$) |
| rref($[A,y]$) | conterá na última coluna a solução |
permite obter as colunas LD e montar todas as soluções |
pouco útil, retornará na última coluna uma parte da matriz identidade |
Outro comando que pode ser usado é o inv(A) * y, porém, ele só funcionará se existir a inversa da matriz $ \mathbf{A} $, o que obrigatoriamente só ocorre se a matriz for quadrada e tiver posto cheio ($ p= m = n $).