Universidade do Estado do Rio de Janeiro
Instituto de Química
Prof André Luís Alberton

Modelagem de Sistemas

Modelagem dinâmica de leitos isotérmicos

Para ilustrar a ideia geral do procedimento, considere uma coluna de bolhas co-corrente. Nesta coluna, gás e líquido escoam em um mesmo sentido, podendo haver troca de massa e calor entre as fases. A ideia da modelagem consiste em considerar duas fases separadas, com escoamentos 'independentes', embora possam trocar calor e massa. Esta ideia está ilustrada na Figura 1.

De forma geral, podemos então nos referir à um caso com duas fases, fase $ \alpha $ e fase $ \beta $, como segue.

Balanço material

Considere duas fases $ \alpha, \ \beta $. Seja a taxa de transferência de massa definida como $ \alpha \rightarrow \beta $, ou seja:

$$ \left( \begin{array}{c} \text{ Taxa} \cr \text{de transf} \cr \text{de massa} \end{array} \right) : {\alpha \rightarrow \beta} $$

Os balanços materiais para uma espécie $ i $ qualquer podem ser escritos para as fases, para um elemento infinitesimal qualquer de volume ficam:

$$ \rm{Fase \ \alpha} $$$$ \left( \begin{array}{c} \text{Taxa de } \cr \text{ acúmulo} \end{array} \right)_i^{\alpha} = \left( \begin{array} \text{Vazão} \cr \text{que entra} \end{array} \right) _i^{\alpha} - \left( \begin{array} \text{Vazão} \cr \text{que sai} \end{array} \right) _i^{\alpha} + \left( \begin{array}{c} \text {Taxa de } \cr \text{ formação } \cr \text{ por reação } \end{array}\right)_i ^{\alpha} - \left( \begin{array}{c} \text{ Taxa} \cr \text{de transf} \cr \text{de massa} \end{array} \right)_i^{\alpha} $$$$ \rm{Fase \ \beta} $$$$ \left( \begin{array}{c} \text{Taxa de } \cr \text{ acúmulo} \end{array} \right)_i^{\beta} = \left( \begin{array} \text{Vazão} \cr \text{que entra} \end{array} \right) _i^{\beta} - \left( \begin{array} \text{Vazão} \cr \text{que sai} \end{array} \right) _i^{\beta} + \left( \begin{array}{c} \text {Taxa de } \cr \text{ formação } \cr \text{ por reação } \end{array}\right)_i ^{\beta} \color{blue}{+} \left( \begin{array}{c} \text{ Taxa} \cr \text{de transf} \cr \text{de massa} \end{array} \right)_i^{\beta} $$

O balanço pode ser feito para uma fase qualquer, digamos, a fase $ \alpha $.

Hipóteses:

• (i) fluxo difusivo dado pela lei de Fick ($- D_i^{\alpha} \frac{ \partial C_i^{\alpha}}{\partial z} $)
• (ii) Difusividade da espécie i constante $ D_i^{\alpha} = cte $
• (iii) Área transversal constante $ A_t^{\alpha} = cte $
• (iii) Área interfacial por volume da fase $ \alpha $ homogênea em todo o volume $ a^{\alpha} = \frac{A_{\alpha,\beta}}{V^{\alpha}} $
• (iv) o volume da fase não muda com o tempo

Com base nisto, o balanço para um elemento de volume $ \Delta V^{\alpha} $ compreendido entre $ z $ e $ z + \Delta z $ fica:

$$ \underbrace{\left( \begin{array}{c} \text{Taxa de } \cr \text{ acúmulo} \end{array} \right)_i^{\alpha}}_{ \Delta V^{\alpha} \cdot \frac{\partial C_i^{\alpha}}{\partial t}} = \underbrace{\left( \begin{array} \text{Vazão} \cr \text{que entra} \end{array} \right) _i^{\alpha}}_{\left. \left( - D_i^{\alpha} \cdot \frac{ \partial C_i^{\alpha} }{\partial z} + u^{\alpha} \cdot C_i^{\alpha} \right) \right|_{entra}} - \underbrace{\left( \begin{array} \text{Vazão} \cr \text{que sai} \end{array} \right) _i^{\alpha}}_{\left. \left( - D_i^{\alpha} \cdot \frac{ \partial C_i^{\alpha} }{\partial z} + u \cdot C_i^{\alpha} \right) \right|_{sai}} + \underbrace{\left( \begin{array}{c} \text {Taxa de } \cr \text{ formação } \cr \text{ por reação } \end{array}\right)_i ^{\alpha}}_{r_i \cdot \Delta V^{\alpha}} - \underbrace{\left( \begin{array}{c} \text{ Taxa} \cr \text{de transf} \cr \text{de massa} \end{array} \right)_i^{\alpha}}_{ J_i \cdot A_{\alpha, \beta}} $$

Ou seja:

$$ \Delta V^{\alpha} \cdot \frac{\partial C_i^{\alpha}}{\partial t} = \left. \left( - D_i^{\alpha} \cdot \frac{ \partial C_i^{\alpha} }{\partial z} + u^{\alpha} \cdot C_i^{\alpha} \right) \right|_{entra} \cdot A_t^{\alpha} - \left. \left( - D_i^{\alpha} \cdot \frac{ \partial C_i^{\alpha} }{\partial z} + u^{\alpha} \cdot C_i^{\alpha} \right) \right|_{sai} \cdot A_t^{\alpha} + r_i^{\alpha} \cdot \Delta V^{\alpha} - J_i \cdot A_{\alpha, \beta} $$

Rearranajando e dividindo por $ \Delta V^{\alpha} = A_t^{\alpha} \cdot \Delta z $:

$$ \frac{\partial C^{\alpha}_i}{\partial t} = \frac{ \left. \left( - D_i^{\alpha} \cdot \frac{ \partial C_i^{\alpha} }{\partial z} + u \cdot C_i^{\alpha} \right) \right|_{entra} \cdot A_t^{\alpha} - \left. \left( - D_i^{\alpha} \cdot \frac{ \partial C_i^{\alpha} }{\partial z} + u^{\alpha} \cdot C_i^{\alpha} \right) \right|_{sai} \cdot A_t^{\alpha}}{ A_t^{\alpha} \cdot \Delta z } + r_i^{\alpha} - J_i \cdot \frac{ A_{\alpha, \beta} }{ \Delta V^{\alpha} } $$

Definindo $ a^{\alpha} = \frac{ A_{\alpha, \beta} }{ \Delta V^{\alpha} } $ . Simplificando fica:

$$ \frac{\partial C_i^{\alpha}}{\partial t} = \frac{ \left. \left( - D_i^{\alpha} \cdot \frac{ \partial C_i^{\alpha} }{\partial z} + u^{\alpha} \cdot C_i^{\alpha} \right) \right|_{entra} - \left. \left( - D_i^{\alpha} \cdot \frac{ \partial C_i^{\alpha} }{\partial z} + u^{\alpha} \cdot C_i^{\alpha} \right) \right|_{sai} }{ \Delta z } + r_i - J_i \cdot a^{\alpha} $$

Rearranjando e tomando o limite com $ \Delta z \rightarrow 0 $, tem-se:

$$ \frac{\partial C_i^{\alpha}}{\partial t} = \lim_{\Delta z \rightarrow 0} D_i^{\alpha} \cdot \frac{ \left( \left. \frac{\partial C_i^{\alpha}}{\partial z} \right|_{z + \Delta z} - \left. \frac{\partial C_i^{\alpha}}{\partial z} \right|_{z} \right) }{\Delta z} - \frac{ \left. \left( u^{\alpha} \cdot C_i^{\alpha} \right) \right) |_{z + \Delta z} - \left. \left( u^{\alpha} \cdot C^{\alpha} \right) \right|_{z} }{\Delta z} + r_i^{\alpha} - J_i \cdot a^{\alpha} $$

Que por sua vez, fica:

$$ \frac{\partial C_i^{\alpha}}{\partial t} = D_i^{\alpha} \cdot \frac{ \partial^2{C_i^{\alpha}}}{\partial z^2} - \frac{ \partial \left( u^{\alpha} \cdot C_i^{\alpha} \right) }{ \partial z} + r_i^{\alpha} - J_i \cdot a^{\alpha} $$

O desenvolvimento acima pode ser desenvolvido para a fase $ \beta $. O balanço material para ambas as fases leva às seguintes equações diferenciais parciais:

$$ \rm{Fase \ \alpha} $$$$ \frac{\partial C_i^{\alpha}}{\partial t} = D_i^{\alpha} \cdot \frac{ \partial^2{C_i^{\alpha}}}{\partial z^2} - \frac{ \partial \left( u^{\alpha} \cdot C_i^{\alpha} \right) }{ \partial z} + r_i^{\alpha} - J_i \cdot a^{\alpha} $$$$ \rm{Fase \ \beta, \ em \ vermelho, \ cocorrente, \ em \ azul \ contracorrente} $$$$ \frac{\partial C_i^{\beta}}{\partial t} = \begin{array}{c}{\color{red}+} \cr {\color{blue}-} \end{array} \left( D_i^{\beta} \cdot \frac{ \partial^2{C_i^{\beta}}}{\partial z^2} \right) \begin{array}{c}{\color{red}-} \cr {\color{blue}+} \end{array} \left( \frac{ \partial \left( | u^{\beta} | \cdot C_i^{\beta} \right) }{ \partial z} \right) + r_i^{\beta} + J_i \cdot a^{\beta} $$

Valem dois comentários sobre a equação da fase $ \beta $.

• o modo contracorrente muda o sinal dos termos de convecção e difusão (admitindo a velocidade dada em módulo).

• a área por volume das fases $ a^{\alpha}, a^{\beta} $ são distintas, uma vez que são resultado, respectivamente da divisão da área interfacial $ A_{\alpha,\beta} $ divididas pelo volume da fase $ \alpha $ e pelo volume da fase $ \beta $, ou seja:

  $$ \begin{array} {ccc} a^{\alpha} = \frac{ A_{\alpha,\beta} }{V^{\alpha}} & , & a^{\beta} = \frac{ A_{\alpha,\beta} }{V^{\beta}} \end{array} $$

Por vezes, encontram-se correlações para determinar a área por unidade de volume do equipamento como um todo (somando o volume das fases). Tomando as definições $ a^{\alpha}, a^{\beta} $ e multiplicando-se e dividindo ambos os termos pelo volume do equipamento com as duas fases, tem-se:

$$ \text{Para a fase } \alpha: $$$$ a^{\alpha} = \frac{ A_{\alpha,\beta} }{V^{\alpha}} \times \frac{ V_{\alpha+ \beta} }{V^{\alpha + \beta}} = \cdot \underbrace{ \frac{ A_{\alpha,\beta} }{V^{\alpha + \beta}}}_{a^{\alpha+\beta}} \cdot \underbrace{ \frac{ V^{\alpha,\beta} }{V^{\alpha}}}_{ \frac{1}{ \sigma^{\alpha} } } = a^{\alpha+\beta} \cdot \frac{1}{ \sigma^{\alpha} } $$$$ \text{Para a fase } \beta: $$$$ a^{\beta} = \frac{ A_{\alpha,\beta} }{V^{\beta}} \times \frac{ V_{\alpha+ \beta} }{V^{\alpha + \beta}} = \cdot \underbrace{ \frac{ A_{\alpha,\beta} }{V^{\alpha + \beta}}}_{a^{\alpha+\beta}} \cdot \underbrace{ \frac{ V^{\alpha,\beta} }{V^{\beta}}}_{ \frac{1}{ \sigma^{\alpha} } } = a^{\alpha+\beta} \cdot \frac{1}{ \sigma^{\beta} } $$

Em que $\sigma^{\alpha}$, $\sigma^{\beta}$ correspondem, às frações volumétricas das fases $ \alpha, \ \beta $, respectivamente.

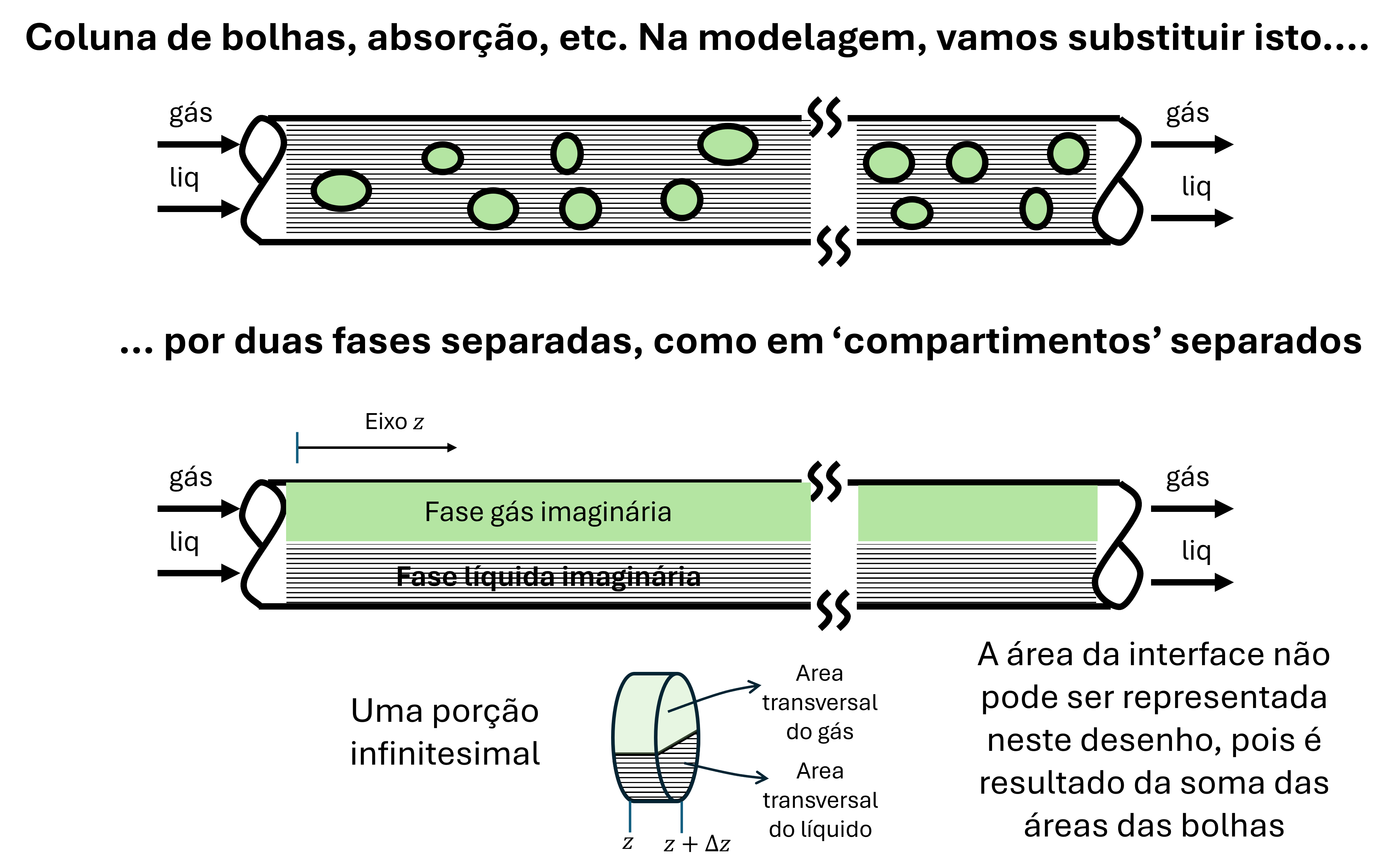
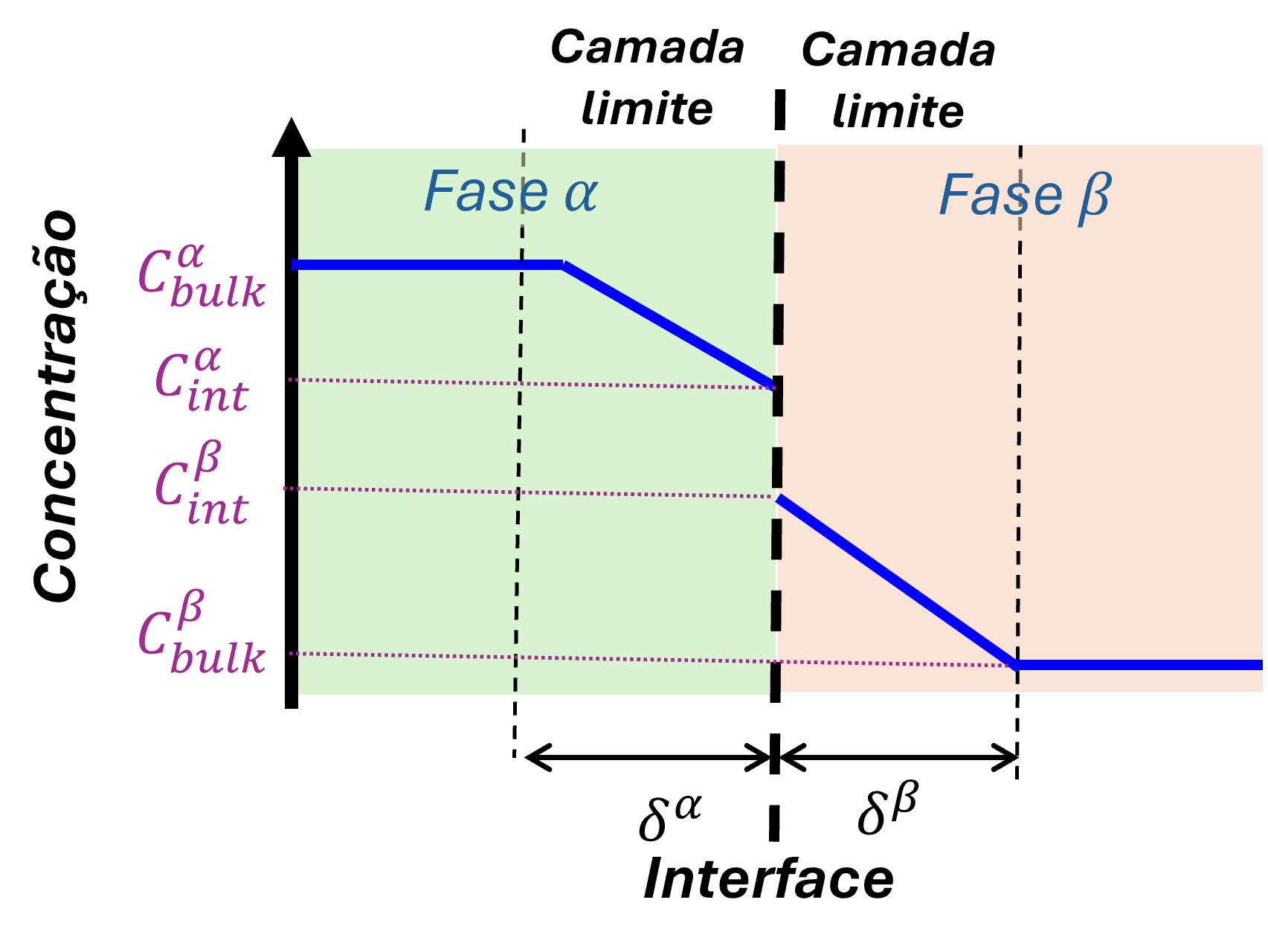
Adimensionalizando o modelo

Adotando um comprimento adimensional:

$$ \eta = \frac{z}{L} $$

Definindo também uma concentração total adimensional $ \phi_i $ e uma velocidade adimensional $ \mathscr(v) $ escritas como (tomaremos como referência valores da fase $ \alpha $, para ambas as fases):

$$\begin{array}{ccc} \phi_i^{\alpha} = \frac{ C_i^{\alpha} }{ C_0^{\alpha} } & & \phi_i^{\beta} = \frac{ C_i^{\beta} }{ C_0^{\alpha} } \cr \mathscr{v^{\alpha}} = \frac{u^{\alpha}}{u_0^{\alpha}} & & \mathscr{v^{\beta}} = \frac{u^{\beta}}{u_0^{\alpha}} \end{array} $$

Nas relações acima, $C_0^{\alpha}$ é a concentração total em $ z=0 $ e $ u_0^{\alpha} $ é a velocidade inicial da mistura em $ z=0 $ para a fase $\alpha$.

As equações para as fases $ \alpha, \beta $ ficam então (vamos adotar o sentido co-corrente para as fases):

$$ C_0^{\alpha} \cdot \frac{\partial \phi_i^{\alpha}}{\partial t} = \frac{ D_i^{\alpha} \cdot C_0^{\alpha}}{L^2} \cdot \frac{ \partial^2{\phi_i^{\alpha}}}{\partial \eta^2} - \frac{ u_0^{\alpha} \cdot C_0^{\alpha} }{L} \cdot \frac{\partial \left( \mathscr{v^{\alpha}} \cdot \phi_i^{\alpha} \right) }{ \partial \eta} + r_i^{\alpha} - J_i \cdot a^{\alpha} $$$$ C_0^{\alpha} \cdot \frac{\partial \phi_i^{\beta}}{\partial t} = \frac{ D_i^{\beta} \cdot C_0^{\alpha}}{L^2} \cdot \frac{ \partial^2{\phi_i^{\beta}}}{\partial \eta^2} - \frac{ u_0^{\alpha} \cdot C_0^{\alpha} }{L} \cdot \frac{\partial \left( \mathscr{v^{\beta}} \cdot \phi_i^{\beta} \right) }{ \partial \eta} + r_i^{\beta} - J_i \cdot a^{\beta} $$

Adotando também um tempo adimensional (também considerando a velocidade da fase $ \alpha $ como referência):

$$ \tau = \frac{t \cdot u_0^{\alpha}}{L} $$

Tem-se, assim, para ambas as fases:

$$ \frac{C_0^{\alpha} \cdot u_0^{\alpha}}{L} \cdot \frac{\partial \phi_i^{\alpha}}{\partial \tau} = \frac{ D_i^{\alpha} \cdot C_0^{\alpha} }{L^2} \cdot \frac{ \partial^2{\phi_i^{\alpha}}}{\partial \eta^2} - \frac{ u_0^{\alpha} \cdot C_0^{\alpha} }{L} \cdot \frac{ \partial \left( \mathscr{v^{\alpha}} \cdot \partial \phi_i^{\alpha} \right) }{ \partial \eta} + r_i^{\alpha} - J_i \cdot a^{\alpha} $$$$ \frac{C_0^{\alpha} \cdot u_0^{\alpha}}{L} \cdot \frac{\partial \phi_i^{\beta}}{\partial \tau} = \frac{ D_i^{\beta} \cdot C_0^{\alpha} }{L^2} \cdot \frac{ \partial^2{\phi_i^{\beta}}}{\partial \eta^2} - \frac{ u_0^{\alpha} \cdot C_0 }{L} \cdot \frac{ \partial \left( \mathscr{v^{\beta}} \cdot \partial \phi_i^{\beta} \right) }{ \partial \eta} + r_i^{\beta} + J_i \cdot ^{\beta} $$

Multiplicando a equação toda por $ \frac{L}{C_0^{\alpha} \cdot u_0^{\alpha}} $, tem-se:

$$ \frac{\partial \phi_i^{\alpha}}{\partial \tau} = \frac{ D_i^{\alpha} }{L \cdot u_0^{\alpha}} \cdot \frac{ \partial^2{\phi_i^{\alpha}}}{\partial \eta^2} - \frac{ \partial \left( \mathscr{v^{\alpha}} \cdot \phi_i^{\alpha} \right) }{ \partial \eta} + \frac{L}{C_0^{\alpha} \cdot u_0^{\alpha}} \cdot \left( r_i^{\alpha} - J_i \cdot a^{\alpha} \right) $$$$ \frac{\partial \phi_i^{\beta}}{\partial \tau} = \frac{ D_i^{\beta} }{L \cdot u_0^{\alpha}} \cdot \frac{ \partial^2{\phi_i^{\beta}}}{\partial \eta^2} - \frac{ \partial \left( \mathscr{v^{\beta}} \cdot \phi_i^{\beta} \right) }{ \partial \eta} + \frac{L}{C_0^{\alpha} \cdot u_0^{\alpha}} \cdot \left( r_i^{\beta} + J_i \cdot a^{\beta} \right) $$

O número de Peclet é definido como:

$$ Pe_i^{\alpha} = \frac{ L \cdot u_0^{\alpha} }{D_i^{\alpha}} $$$$ Pe_i^{\beta} = \frac{ L \cdot u_0^{\alpha} }{D_i^{\beta}} $$

Assim, para as fases, tem-se:

$$ \frac{\partial \phi_i^{\alpha}}{\partial \tau} = \frac{ 1 }{Pe_i^{\alpha}} \cdot \frac{ \partial^2{\phi_i^{\alpha}}}{\partial \eta^2} - \frac{ \partial \left( \mathscr{v^{\alpha}} \cdot \phi_i^{\alpha} \right) }{ \partial \eta} - \frac{L}{C_0^{\alpha} \cdot u_0^{\alpha}} \cdot \left( r_i^{\alpha} - J_i \cdot a^{\alpha} \right) $$$$ \frac{\partial \phi_i^{\beta}}{\partial \tau} = \frac{ 1 }{Pe_i^{\beta}} \cdot \frac{ \partial^2{\phi_i^{\beta}}}{\partial \eta^2} - \frac{ \partial \left( \mathscr{v^{\beta}} \cdot \phi_i^{\beta} \right) }{ \partial \eta} + \frac{L}{C_0^{\alpha} \cdot u_0^{\alpha}} \cdot \left( r_i^{\beta} + J_i \cdot a^{\beta} \right) $$

Além disto, ao multiplicar e dividir $ \frac{L}{C_0^{\alpha} \cdot u_0^{\alpha}} $ pela área transversal da fase $\alpha$, dada por $ A_t^{\alpha} $, tem-se:

$$ \frac{L }{C_0^{\alpha} \cdot u_0^{\alpha} } \cdot \frac{A_t^{\alpha}}{A_t^{\alpha}} = \frac{V^{\alpha}}{F_0^{\alpha} } $$

Em que $ V^{\alpha} $ é o volume do reator da fase $ \alpha $, e $F_0^{\alpha}$ é a vazão molar da entrada na fase $ \alpha $ do reator no tempo $ t = 0 $. Assim, a equação final fica:

$$ \frac{\partial \phi_i^{\alpha}}{\partial \tau} = \frac{ 1 }{Pe_i^{\alpha}} \cdot \frac{ \partial^2{\phi_i^{\alpha}}}{\partial \eta^2} - \frac{ \partial \left( \mathscr{v^{\alpha}} \cdot \phi_i^{\alpha} \right) }{ \partial \eta} - \frac{V^{\alpha}}{F_0^{\alpha}} \cdot \left( r_i^{\alpha} - J_i \cdot a^{\alpha} \right) $$$$ \frac{\partial \phi_i^{\beta}}{\partial \tau} = \frac{ 1 }{Pe_i^{\beta}} \cdot \frac{ \partial^2{\phi_i^{\beta}}}{\partial \eta^2} - \frac{ \partial \left( \mathscr{v^{\beta}} \cdot \phi_i^{\beta} \right) }{ \partial \eta} + \frac{V^{\alpha}}{F_0^{\alpha}} \cdot \left( r_i^{\beta} - J_i \cdot a^{\beta} \right) $$

Cujas condições de contorno ficam:

$$ \rm{Fase \ \alpha} $$\begin{equation} \begin{cases} \rm{Condições \ de \ contorno \ típicas} \\ \left. \phi_i^{\alpha} \right|_{(\tau, \eta = 0 )} = \phi_{i,0}^{\alpha} \\ \left. \frac{ \partial \phi_i^{\alpha} }{ \partial \eta } \right|_{ (\tau, \eta = 1 )} = 0 \ , \text{ou outra condição} \\ \rm{Condições \ iniciais} \\ \left. \phi_i^{\alpha} \right|_{(\tau=0, \eta>0 )} = 0 \\ \end{cases} \end{equation}$$ \rm{Fase \ \beta, \ co-corrente} $$\begin{equation} \begin{cases} \rm{Condições \ de \ contorno \ típicas} \\ \left. \phi_i^{\beta} \right|_{(\tau, \eta = 0 )} = \phi_{i0}^{\beta} \\ \left. \frac{ \partial \phi_i^{\beta} }{ \partial \eta } \right|_{ (\tau, \eta = 1 )} = 0 \ , \text{ou outra condição}\\ \rm{Condições \ iniciais} \\ \left. \phi_i^{\beta} \right|_{(\tau=0, \eta>0 )} = 0 \\ \end{cases} \end{equation}

Comentários sobre a formulação acima

Sobre as hipóteses

A formulação acima é relativamente bastante geral. Neste momento as hipóteses simplificadoras de maior peso são: a Hipótese (ii), que assume Difusividade da espécie i constante $D_i$ = cte e a Hipótese (iv) que assume volume das fases constante.

Sobre a primeira condição de contorno

Outro comentário importante diz respeito às condições de contorno. A primeira condição de contorno pode ser adotada a partir do conhecimento da concentração no início do leito, conforme representado. Outra forma mais suave da condição de contorno consiste em considerar a difusão no início do leito na forma, (também conhecida como condição de Danckwert, 'emprestada de um reator tubular'). Estas duas condições estão ilustrados para a fase $ \alpha $:

$$ \text{Formas típicas para a primeira condição de contorno} $$$$ \left. \phi_i^{\alpha} \right|_{(\tau, \eta = 0 )} = \phi_{i 0}^{\alpha} \\ \text{ou} \\ \\ u_0^{\alpha} \cdot \phi_{i,0}^{\alpha} = \left. \left( u_0^{\alpha} \cdot C_i + D_i^{\alpha} \frac{ \partial \phi_i^{\alpha} }{ \partial \eta } \right) \right|_{ (\tau, \eta = 0 )} , \ \ \text{ou condição de Danckwert} $$

Sobre a segunda condição de contorno e o problema da fronteira livre

Já formas típicas para a segunda condição de contorno dependem fortemente do problema. Por exemplo, considere uma possibilidade (condição de Danckwert, 'emprestada de um reator tubular'):

$$ \text{Forma típica da segunda condição de contorno} $$$$ \left. \frac{ \partial \phi_i }{ \partial \eta } \right|_{ (\tau, \eta = 1 )} = 0 $$

Esta condição surge de se acreditar que o equipamento é 'longo' o suficiente para que ao final sua composição não sofra mais alteração. Para muitos sistemas, como o sistema de adsorção, esta condição é claramente inconsistente ao longo do tempo, pois haverá uma derivada não nula assim que a 'frente de concentração' atingir o final do equipamento. Na literatura é frequente encontrar trabalhos que empregam esta condição (Shafeeyan et al., 2014), mesmo sendo passível de discussão. Este é um problema de fronteira livre, havendo formas de propor a regularização para o desconhecimento da segunda condição de contorno. Uma forma de contornar este problema em colunas de adsorção por exemplo, é apresentada por Myers et al. (2021, 2023) por exemplo, que propõem uma mudança de variável em colunas de adsorção, de que a concentração seja nula em uma frente de escoamento, uma variável em função do tempo, proporcional à velocidade de escoamento.

De forma mais geral, esta condição de contorno é substituída por alguma outra relação, como por exemplo, uma aproximação de uma função de $ \phi_i $ em função de $ \eta $ na parte final do leito, extrapolando para $ \eta = 1 $. Contudo, é necessário salientar que é requerido uma análise particularizada do problema em questão, que deve estar associada ao método de resolução adotado para a solução das EPDs.

Sobre a taxa de transferência de massa

Outro ponto relevante diz respeito à taxa de transferência de massa, sendo tipicamente adotada a fórmula:

$$ J_i = k_i^{TM} \cdot \left( C_i^{\alpha}- C_i^{\beta} \right) $$

em que $ k_i^{TM} $ é a constante de transferência de massa.

Vejamos então este caso particular, mas bastante abrangente.

Caso prático, sem reação, taxa de TM dada pela diferença de concentrações nas fases

Neste caso, não há reação química $ r_i = 0 $ e a transferência de massa dada pela equação:

$$ J_i = k_i^{TM} \cdot \left( C_i^{\alpha}- C_i^{\beta} \right) $$

A equação original fica então:

$$ \frac{\partial \phi_i^{\alpha}}{\partial \tau} = \frac{ 1 }{Pe_i^{\alpha}} \cdot \frac{ \partial^2{\phi_i^{\alpha}}}{\partial \eta^2} - \frac{ \partial \left( \mathscr{v^{\alpha}} \cdot \phi_i^{\alpha} \right) }{ \partial \eta} - \frac{V^{\alpha}}{F_0^{\alpha}} \cdot k_i^{TM} \cdot a^{\alpha} \cdot \left( C_i^{\alpha}- C_i^{\beta} \right) $$$$ \frac{\partial \phi_i^{\beta}}{\partial \tau} = \frac{ 1 }{Pe_i^{\beta}} \cdot \frac{ \partial^2{\phi_i^{\beta}}}{\partial \eta^2} - \frac{ \partial \left( \mathscr{v^{\beta}} \cdot \phi_i^{\beta} \right) }{ \partial \eta} + \frac{V^{\alpha}}{F_0^{\alpha}} \cdot k_i^{TM} \cdot a^{\beta} \cdot \left( C_i^{\alpha}- C_i^{\beta} \right) $$

Ao adotar a normalização para as concentrações, usando $ C_0^{\alpha} $ como referência, tem-se:

$$ \frac{\partial \phi_i^{\alpha}}{\partial \tau} = \frac{ 1 }{Pe_i^{\alpha}} \cdot \frac{ \partial^2{\phi_i^{\alpha}}}{\partial \eta^2} - \frac{ \partial \left( \mathscr{v^{\alpha}} \cdot \phi_i \right) }{ \partial \eta} - \frac{V^{\alpha} \cdot C_0^{\alpha}}{F_0^{\alpha}} \cdot k_i^{TM} \cdot a^{\alpha} \cdot \left( \phi_i^{\alpha}- \phi_i^{\beta} \right) $$$$ \frac{\partial \phi_i^{\beta}}{\partial \tau} = \frac{ 1 }{Pe_i^{\beta}} \cdot \frac{ \partial^2{\phi_i}^{\beta}}{\partial \eta^2} - \frac{ \partial \left( \mathscr{v^{\beta}} \cdot \phi_i^{\beta} \right) }{ \partial \eta} + \frac{V^{\alpha} \cdot C_0^{\alpha}}{F_0^{\alpha}} \cdot k_i^{TM} \cdot a^{\beta} \cdot \left( \phi_i^{\alpha}- \phi_i^{\beta} \right) $$

O termo $ \frac{V^{\alpha} \cdot C_0^{\alpha}}{F_0^{\alpha}} $ pode se simplificado, pois $ F_0^{\alpha} = C_0^{\alpha} \cdot v_0^{\alpha} $; assim o termo fica $ \frac{V \cdot C_0^{\alpha}}{C_0^{\alpha} \cdot v_0^{\alpha}} = \frac{V^{\alpha}}{v_0^{\alpha}} = \mathcal{T}^{\alpha} $, em que $ \mathcal{T}^{\alpha} $ é o tempo de residência do reator na fase $ \alpha $. Assim, a equação fica:

$$ \frac{\partial \phi_i^{\alpha}}{\partial \tau} = \frac{ 1 }{Pe_i^{\alpha}} \cdot \frac{ \partial^2{\phi_i^{\alpha}}}{\partial \eta^2} - \frac{ \partial \left( \mathcal{v^{\alpha}} \cdot \phi_i^{\alpha} \right) }{ \partial \eta} - k_i^{TM} \cdot a^{\alpha} \cdot \mathcal{T}^{\alpha} \cdot \left( \phi_i^{\alpha}- \phi_i^{\beta} \right) $$$$ \frac{\partial \phi_i^{\beta}}{\partial \tau} = \frac{ 1 }{Pe_i^{\beta}} \cdot \frac{ \partial^2{\phi_i^{\beta}}}{\partial \eta^2} - \frac{ \partial \left( \mathcal{v^{\beta}} \cdot \phi_i^{\beta} \right) }{ \partial \eta} + k_i^{TM} \cdot a^{\beta} \cdot \mathcal{T}^{\alpha} \cdot \left( \phi_i^{\alpha}- \phi_i^{\beta} \right) $$

Caso a fase $ \beta $ seja estacionária

Caso a fase $ \beta $ seja estacionária, então, os termos de transporte em $ \eta $ desaparecem. Assim:

$$ \frac{\partial \phi_i^{\alpha}}{\partial \tau} = \frac{ 1 }{Pe_i^{\alpha}} \cdot \frac{ \partial^2{\phi_i^{\alpha}}}{\partial \eta^2} - \frac{ \partial \left( \mathcal{v^{\alpha}} \cdot \phi_i^{\alpha} \right) }{ \partial \eta} - k_i^{TM} \cdot a^{\alpha} \cdot \mathcal{T}^{\alpha} \cdot \left( \phi_i^{\alpha}- \phi_i^{\beta} \right) $$$$ \frac{\partial \phi_i^{\beta}}{\partial \tau} = k_i^{TM} \cdot a^{\beta} \cdot \mathcal{T}^{\alpha} \cdot \left( \phi_i^{\alpha}- \phi_i^{\beta} \right) $$

A complexidade do termo de transferência

O termo de transferência de massa entre fases na Equação apresentada a seguir

$$ J_i = k_i^{TM} \cdot \left( C_i^{\alpha}- C_i^{\beta} \right) $$

pode ser na verdade muito mais complexo. Ele pode envolver transferência de massa entre camadas limites, seguido de relações de equilíbrio. Considere por exemplo, a figura a seguir:

Na figura acima, a transferência de massa ocorre entre o bulk da fase $\alpha $ para a interface da fase $ \alpha $, havendo uma relação de equilíbrio entre a interface das fases $ \alpha, \beta $, seguido de uma transferência de massa da interface da fase $ \beta $ para o bulk da fase $ \beta $. A depender das hipóteses adotadas, a aparente simples solução deste fluxo pode requerer cálculos mais complexos.

Em casos em que se dispõe de valores de constantes de transferência de massa associado a cada uma das fases, e das relações de equilíbrio; adotando-se a hipótese de estado pseudo-estacionário, tem-se:

$$ \text{Fluxo da espécie } i $$$$ J_i = k_i^{\alpha} \cdot \left( C_{i,bulk}^{\alpha} -C_{i,int}^{\alpha} \right) $$$$ \text{Igualdade de transferência de massa entre as fases} $$$$ k_i^{\alpha} \cdot \left( C_{i,bulk}^{\alpha} -C_{i,int}^{\alpha} \right) = k_i^{\beta} \cdot \left( C_{i,int}^{\beta} -C_{i,bulk}^{\beta} \right) $$$$ \text{relação de equilíbrio na interface} $$$$ g^{eq}\left[ C_{i,int}^{\alpha}, C_{i,int}^{\beta} \right] = 0 $$

Este sistema de equações precisaria ser resolvido para determinar o fluxo. Note que, no sistema, a princípio, devem ser conhecidas as concentrações bulk de ambas as fases $ C_{i,bulk}^{\alpha}, \ C_{i,bulk}^{\beta} $. Sobram então três incógnitas, o fluxo propriamente dito, e as cocentrações na interface $ J_i, \ C_{i,int}^{\alpha}, \ C_{i,int}^{\beta} $, que pode ser resolvido pelas três equações acima . A depender da natureza da relação de equilíbrio, procedimentos numéricos complexos podem ser exigidos. Se, por outro lado, a relação de equilíbrio for simples, o sistema pode ser resolvido analiticamente.

Sobre os métodos de resolução das EDPs

A resolução do sistema de equações diferenciais parciais obtidas pode ser feita por diferentes métodos. São apresentadas aqui duas formas associadas ao método das linhas:

• aproximação polinomial de $ \phi_i^{\alpha}, \phi_i^{\beta} $ como um polinômios interpoladores de Lagrange em $ \eta $
• aproximação das derivadas de $ \phi_i^{\alpha}, \phi_i^{\beta} $ por diferenças finitas

No método das linhas, as equações diferenciais parciais são transformadas em equações diferenciais ordinárias em uma variável, no caso, o tempo.

Por aproximação polinomial

Para ilustrar este caso, consider o caso em que a velocidade $ \mathscr{v} $ é constante nas fases. Vamos também ilustrar apenas para a fase $ \alpha $. Precisaremos também omitir o índice associado ao composto $ i $ por clareza, pois os índices nesta seção irão se referir à pontos discretizados em $ \eta $. Assim, a equação da fase $ \alpha $ fica:

$$ \frac{\partial \phi^{\alpha}}{\partial \tau} = \frac{ 1 }{Pe^{\alpha}} \cdot \frac{ \partial^2{\phi^{\alpha}}}{\partial \eta^2} - \mathscr{v^{\alpha}} \cdot \frac{ \partial \phi }{ \partial \eta} - k^{TM} \cdot a^{\beta} \cdot \mathcal{T}^{\alpha}\cdot \left( \phi^{\alpha} - \phi^{\beta} \right) $$

Considerando que $ \phi\left[\tau,\eta\right] $, considerando $N$ pontos de discretização no espaço $ \eta $, o polinômio pode ser aproximado por um polinômio interpolador de Lagrange na forma:

$$\phi_k \left[\tau \right] = \sum_{k=1}^{N}{l_k \left[\eta \right] \cdot \phi_k \left[ \tau \right]} ,\ \ \forall \ k \in (1:N) $$

em que cada $ l_k \left[\eta \right] $ correspondem ao polinômio interpolador de Lagrange na forma:

$$ l_k \left[\eta \right] = \prod_{j =1, \\ j \neq k}^{N}{\frac{\eta-\eta_j}{\eta_k - \eta_j}} \ , \ \ \forall \ k \in (1:N) $$

As incógnitas do problema se tornam, então, os valores de $ \phi_k \left[ \tau \right] $ nos pontos de interpolação. As funções $ l_k \left[\eta \right] $ são apenas funções de $ \eta $. Podemos então calcular as derivadas primeira e segunda dos termos difusivo e convectivo, respectivamente:

$$ \frac{ \partial \phi_k }{ \partial \eta} = \frac{ \sum_{k=1}^{N}{l_k \left[\eta \right] \cdot \phi_k \left[ \tau \right]} }{ \partial \eta} = \sum_{k=1}^{N}{ \phi_k \left[ \tau \right] \cdot \frac{ \partial l_k \left[\eta \right] } { \partial \eta}}, \ \forall \ k \in (1:N) $$

Analogamente, para a derivada segunda:

$$ \frac{ \partial^2 \phi_k }{ \partial \eta^2 } = \frac{ \sum_{k=1}^{N}{l_k \left[\eta \right] \cdot \phi_k \left[ \tau \right]} }{ \partial^2 \eta^2 } = \sum_{k=1}^{N}{ \phi_k \left[ \tau \right] \cdot \frac{ \partial^2 l_k \left[\eta \right] } { \partial \eta^2 }}, \ \ \forall \ k \in (1:N) $$

Aplica-se a equação diferencial aos pontos $ \eta = \left( \eta_2, \eta_3, ..., \eta_{N-1}, \eta_N \right) $. O primeiro ponto ($ \eta_1 = 0$ ) é tomado a partir da condição informada como a primeira condição de contorno. Tem-se então o seguinte sistema:

$$ \text{Ponto } \eta = \eta_1 $$$$\frac{\partial \phi_1^{\alpha}}{\partial \tau} = 0 $$$$ \text{Ponto } \eta = \eta_2 $$$$ \frac{\partial \phi_2^{\alpha}}{\partial \tau} = \frac{ 1 }{Pe^{\alpha}} \cdot \sum_{k=1}^{N}{ \phi_k \left[ \tau \right] \cdot \left. \frac{ \partial^2 l_k \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_2} } - \mathscr{v^{\alpha}} \cdot \sum_{k=1}^{N}{ \phi_k \left[ \tau \right] \cdot \left. \frac{ \partial l_k \left[\eta \right] } { \partial \eta} \right|_{\eta_2}} - k^{TM} \cdot a^{\beta} \cdot \mathcal{T}^{\alpha} \cdot \left( \phi_2^{\alpha}- \phi_2^{\beta} \right) $$$$ \text{Ponto } \eta = \eta_3 $$$$ \frac{\partial \phi_3^{\alpha}}{\partial \tau} = \frac{ 1 }{Pe^{\alpha}} \cdot \sum_{k=1}^{N}{ \phi_k \left[ \tau \right] \cdot \left. \frac{ \partial^2 l_k \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_3} } - \mathscr{v^{\alpha}} \cdot \sum_{k=1}^{N}{ \phi_k \left[ \tau \right] \cdot \left. \frac{ \partial l_k \left[\eta \right] } { \partial \eta} \right|_{\eta_3}} - k^{TM} \cdot a^{\beta} \cdot \mathcal{T}^{\alpha} \cdot \left( \phi_3^{\alpha}- \phi_3^{\beta} \right) $$$$ ... $$$$ \text{Ponto } \eta = \eta_{N-1} $$$$ \frac{\partial \phi_{N-1}^{\alpha}}{\partial \tau} = \frac{ 1 }{Pe^{\alpha}} \cdot \sum_{k=1}^{N}{ \phi_k \left[ \tau \right] \cdot \left. \frac{ \partial^2 l_k \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_{N-1}} } - \mathscr{v^{\alpha}} \cdot \sum_{k=1}^{N}{ \phi_k \left[ \tau \right] \cdot \left. \frac{ \partial l_k \left[\eta \right] } { \partial \eta} \right|_{\eta_{N-1}}} - k^{TM} \cdot a^{\beta} \cdot \mathcal{T}^{\alpha} \cdot \left( \phi_{N-1}^{\alpha}- \phi_{N-1}^{\beta} \right) $$$$ \text{Ponto } \eta = \eta_N $$$$ \frac{\partial \phi_N^{\alpha}}{\partial \tau} = \frac{ 1 }{Pe^{\alpha}} \cdot \sum_{k=1}^{N}{ \phi_k \left[ \tau \right] \cdot \left. \frac{ \partial^2 l_k \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_N} } - \mathscr{v^{\alpha}} \cdot \sum_{k=1}^{N}{ \phi_k \left[ \tau \right] \cdot \left. \frac{ \partial l_k \left[\eta \right] } { \partial \eta} \right|_{\eta_N}} - k^{TM} \cdot a^{\beta} \cdot \mathcal{T}^{\alpha} \cdot \left( \phi_N^{\alpha}- \phi_N^{\beta} \right) $$

O sistema de equações pode ser escrito na forma matricial como:

$$ \frac{\partial }{\partial \tau} \begin{pmatrix} \phi_1^{\alpha} \cr \phi_2^{\alpha} \cr \phi_3^{\alpha} \cr ... \cr \phi_{N-1}^{\alpha} \cr \phi_N^{\alpha} \end{pmatrix} = \mathbf{B} \cdot \begin{pmatrix} \phi_1^{\alpha} \cr \phi_2^{\alpha} \cr \phi_3^{\alpha} \cr ... \cr \phi_{N-1}^{\alpha} \cr \phi_N^{\alpha} \end{pmatrix} - \mathbf{A} \cdot \begin{pmatrix} \phi_1^{\alpha} \cr \phi_2^{\alpha} \cr \phi_3^{\alpha} \cr ... \cr \phi_{N-1}^{\alpha} \cr \phi_N^{\alpha} \end{pmatrix} + k^{TM} \cdot a^{\beta} \cdot \mathcal{T}^{\alpha} \cdot \begin{pmatrix} 0 \cr \phi_2^{\alpha} - \phi_2^{\beta} \cr \phi_3^{\alpha}-\phi_3^{\beta} \cr ... \cr \phi_{N-1}^{\alpha} - \phi_{N-1}^{\beta} \cr \phi_N^{\alpha} - \phi_N^{\beta} \end{pmatrix} $$

Em que as matrizes $ \mathbf{B}, \ \mathbf{A}$ são escritas como:

$$ \mathbf{B} = \begin{pmatrix} 0 & 0 & 0 & ... & 0 & 0 \cr \left. \frac{ \partial^2 l_1 \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_2} & \left. \frac{ \partial^2 l_2 \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_2} & \left. \frac{ \partial^2 l_3 \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_2} & ... & \left. \frac{ \partial^2 l_{N-1} \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_2} & \left. \frac{ \partial^2 l_N \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_2} \cr \left. \frac{ \partial^2 l_1 \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_3} & \left. \frac{ \partial^2 l_2 \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_3} & \left. \frac{ \partial^2 l_3 \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_3} & ... & \left. \frac{ \partial^2 l_{N-1} \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_3} & \left. \frac{ \partial^2 l_N \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_3} \cr ... \cr \left. \frac{ \partial^2 l_1 \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_{n-1}} & \left. \frac{ \partial^2 l_2 \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_{n-1}} & \left. \frac{ \partial^2 l_3 \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_{N-1}} & ... & \left. \frac{ \partial^2 l_{n-1} \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_{N-1}} & \left. \frac{ \partial^2 l_N \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_{N-1}} \cr \left. \frac{ \partial^2 l_1 \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_N} & \left. \frac{ \partial^2 l_2 \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_N} & \left. \frac{ \partial^2 l_3 \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_N} & ... & \left. \frac{ \partial^2 l_{N-1} \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_N} & \left. \frac{ \partial^2 l_N \left[\eta \right] } { \partial \eta^2 } \right|_{\eta_N} \end{pmatrix} $$$$ \mathbf{A} = \begin{pmatrix} 0 & 0 & 0 & ... & 0 & 0 \cr \left. \frac{ \partial l_1 \left[\eta \right] } { \partial \eta } \right|_{\eta_2} & \left. \frac{ \partial l_2 \left[\eta \right] } { \partial \eta } \right|_{\eta_2} & \left. \frac{ \partial l_3 \left[\eta \right] } { \partial \eta } \right|_{\eta_2} & ... & \left. \frac{ \partial l_{N-1} \left[\eta \right] } { \partial \eta } \right|_{\eta_2} & \left. \frac{ \partial l_N \left[\eta \right] } { \partial \eta } \right|_{\eta_2} \cr \left. \frac{ \partial l_1 \left[\eta \right] } { \partial \eta } \right|_{\eta_3} & \left. \frac{ \partial l_2 \left[\eta \right] } { \partial \eta } \right|_{\eta_3} & \left. \frac{ \partial l_3 \left[\eta \right] } { \partial \eta } \right|_{\eta_3} & ... & \left. \frac{ \partial l_{N-1} \left[\eta \right] } { \partial \eta } \right|_{\eta_3} & \left. \frac{ \partial l_N \left[\eta \right] } { \partial \eta } \right|_{\eta_3} \cr ... \cr \left. \frac{ \partial l_1 \left[\eta \right] } { \partial \eta } \right|_{\eta_{N-1}} & \left. \frac{ \partial l_2 \left[\eta \right] } { \partial \eta } \right|_{\eta_{N-1}} & \left. \frac{ \partial l_3 \left[\eta \right] } { \partial \eta } \right|_{\eta_{N-1}} & ... & \left. \frac{ \partial l_{N-1} \left[\eta \right] } { \partial \eta } \right|_{\eta_{N-1}} & \left. \frac{ \partial l_N \left[\eta \right] } { \partial \eta } \right|_{\eta_{N-1}} \cr \left. \frac{ \partial l_1 \left[\eta \right] } { \partial \eta } \right|_{\eta_N} & \left. \frac{ \partial l_2 \left[\eta \right] } { \partial \eta } \right|_{\eta_N} & \left. \frac{ \partial l_3 \left[\eta \right] } { \partial \eta } \right|_{\eta_N} & ... & \left. \frac{ \partial l_{N-1} \left[\eta \right] } { \partial \eta } \right|_{\eta_N} & \left. \frac{ \partial l_N \left[\eta \right] } { \partial \eta } \right|_{\eta_N} \end{pmatrix} $$

O sistema pode então ser resolvido por um resolvedor de EDO's.

Exemplo

Considere uma coluna de adsorção (fase $ \alpha $ sendo gás e $ \beta $ sendo sólido), sendo dados:

• $ k_i^{TM} \cdot a^{\alpha} \cdot \mathcal{T}^{\alpha} = 0.05 $
• $ Pe_i^{\alpha} = 20 $
• velocidade da fase gás não se modifica $ \mathscr{v^{\alpha}}=1 $

Inicialmente, não contém a espécie que irá se adsorver. Simule o comportamento da espécie de interesse ao longo do leito para diferentes tempos.

Solução por aproximação polinomial

Na solução, a segunda condição de contorno será desprezada, sendo substituída pela aplicação da equação diferencial ao último ponto do leito. O código em Scilab a seguir resolve o problema por aproximação polinomial, considerando $ \phi_i^{\alpha}, \phi_i^{\beta} $ como um polinômios interpoladores de Lagrange em $ \eta $.

clear;clc;close

function f = PolLag(x,xp,yp)
    f = 0
    n = length(xp)
    for i=1:n
        pos = [1:i-1,i+1:n]
        f = f + yp(i)*prod(x-xp(pos))/prod(xp(i)-xp(pos))
    end
endfunction

function f = PolLag_li(x,xp)
    n = length(xp)
    for i=1:n
        pos = [1:i-1,i+1:n]
        f(i) = prod(x-xp(pos))/prod(xp(i)-xp(pos))
    end        
endfunction

function dy = sistemadin(t,y)
    C_alpha = y(1:n)
    C_beta = y(n+1:2*n)
    tx_desap = kTranf*(C_alpha - C_beta)
    // Fase alpha
    dy(1) = 0
    dy(2:n-1) = 1 / Pe* B(2:$-1,:)*C_alpha - A(2:$-1,:)*C_alpha - tx_desap(2:$-1)
    dy(n) = -A($,:)*C_alpha
    // equacoes da massa
    dy(n+1) = 0 
    dy(n+1:2*n) = + tx_desap(1:$)
endfunction


n = 15 // número de pontos no espaço
xp = linspace(0,1,n) // pontos no espaço
for k =1:n
    [a,b] = numderivative(list(PolLag_li,xp),xp(k))
    A(k,:) = a'
    B(k,:) = b'
end


kTranf = 0.05 // cte de transferência
Pe = 20 // número de Peclet
C0din = [0.03;zeros(n-1,1)]
q0din = [zeros(n,1)]
y0din = [C0din;q0din]
t = logspace(0,.5,10)-1
ydin = ode(y0din,0,t,sistemadin)
Cdin = ydin(1:n,:)
qdin = ydin(n+1:2*n,:)

scf()
//plot(t,Cdin)
subplot(1,2,1)
plot(xp,Cdin')
title('Concentração','font_size',5)
xlabel('$ \rm{comprimento \ do \ leito} $','font_size',4,'color','blue')
ylabel('$ \rm{C_{gás}} $','font_size',4,'color','blue')

subplot(1,2,2)
plot(xp,qdin')
title('Fase sólida','font_size',5)
xlabel('$ \rm{comprimento \ do \ leito} $','font_size',4,'color','blue')
ylabel('$ \rm{q_{sol}} $','font_size',4,'color','blue')

hl=legend(string(round(100*t)/100));
// mainpulando as propriedades da legenda
e=gce()
e.font_size = 3
e.legend_location ='in_upper_right'

O resultados estão apresentado a seguir:

Conforme pode ser observado, por volta do tempo adimensional de $ 0.47 $, a operação da coluna deverá ser interrompida, pois o composto a ser adsorvido começará a sair da coluna.

Referências

• Myers, T.G., Font, F., Hennessy, M.G., 2020. Mathematical modelling of carbon capture in a packed column by adsorption. Applied Energy 278, 115565. https://doi.org/10.1016/j.apenergy.2020.115565

• Myers, T.G., Cabrera-Codony, A., Valverde, A., 2023. On the development of a consistent mathematical model for adsorption in a packed column (and why standard models fail). International Journal of Heat and Mass Transfer 202, 123660. https://doi.org/10.1016/j.ijheatmasstransfer.2022.123660

• Shafeeyan, M.S., Wan Daud, W.M.A., Shamiri, A., 2014. A review of mathematical modeling of fixed-bed columns for carbon dioxide adsorption. Chemical Engineering Research and Design 92, 961–988. https://doi.org/10.1016/j.cherd.2013.08.018